Зорич (стр.60): если
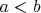
, то найдется число

между ними. Эта аксиома полноты прописана также и Фихтенгольца (стр.19). Но далее, когда речь заходит о принципе/аксиоме Архимеда, то Зорич его выводит, а Фихтенгольц объявляет аксиомой, да еще и подчеркивает, что она не выводима из других. Где, т.е. в каком сочетании других аксиомах, зарыта собака? Более того, Зорич (стр. 45), да вроде и другие, утверждают о категоричности аксиом вещественных чисел. Но с другой стороны, если мы обратимся к нестандартному анализу Робинсона, то он являет собой тоже модель упорядоченного поля, как и

, но не изоморфное вещественным числам. В каком месте собака зарыта здесь? Насколько я пока вижу топология для выявления различия между этими моделями не задействуется. Или это не так? Аналогичный вопрос у меня и про сопоставление аксиомы Архимеда выше.
Аксиомы полного упорядоченного поля записываются на языке второго порядка. В нём есть два вида переменных -- переменные

по действительным числам и переменные

по множествам действительных чисел. Когда мы строим модели для теорий в таком языке, мы обычно выбираем множество-носитель

(например, множество действительных чисел) и считаем, что переменные

пробегают по множеству

(всех подмножеств

). При таком определении модели можно доказать, что существует ровно одно полное упорядоченное поле (с точностью до изоморфизма). Но можно расширить понятие модели и не требовать, чтобы

пробегали по ВСЕМ подмножествам. В нестандартной модели

пробегают по некоторому семейству подмножеств, которые называются "внутренними". Аксиома

имеет супремум)
означает "каждое внутреннее множество, ограниченное сверху, имеет супремум". Не все множества внутренние.