Расхождения в решениях задачи на оптимальное время

[Dave Karapetian]

Условие задачи и рисунок:

"Человек, находясь в точке В на расстоянии h от прямого участка дороги (рис. 1), видит в точке А автобус, двигающийся по дороге с постоянной скоростью va. Расстояние от человека до автобуса в этот момент АВ. В каком направлении следует бежать человеку, чтобы оказаться на дороге в точке С с максимальным опережением по
времени по отношению к автобусу? Отношение расстояний $\frac{h}{AB}$ $=$ $\frac{1}{2}$; отношение скоростей человека и автобуса $\frac{vч}{va}$ $=$ $\frac{1}{\sqrt{2}}$".


Непонятна постановка задачи, конкретно смысл вопроса "в каком направлении следует бежать человеку, чтобы оказаться на дороге в точке С с максимальным опережением по времени ".
В ответе приводится оптимальное, а не максимальное значение угла $\varphi$опт при вершине В треуглольника АВС, равное 105 град.
Можно также предположить, что речь идёт об оптимальном угле, направления движения человека, увидевший автобус на расстоянии АВ под искомым углом $\varphi $c АB к некоей точке С, чтобы добраться до неё одновременно с автобусом. Т.е. , автобус и человек должны достичь точки С за одно и то же время Т из точек А и В соотвественно.
На чертеже указаны также угол $\alpha$ при вершине А (в моём решении он не используется, но, вероятно, можно использовать теорему синусов) и "расстояние h до прямого участка дороги". Допускаю, что это высота треугольника АВС, опущенная из вершины В на отрезок АС.
Точку пересечения h с АС обозначаем буквой D.
Положим, что высота h делит искомый угол $\varphi$ на две составляющие: углы $\varphi$1 и $\varphi$2. Т.е. $\varphi$1 $+$ $\varphi$2 $=$ $\varphi$.

Из данного в условии соотношения высоты h и стороны АВ можно сделать вывод, что угол $\alpha$ $= $ 30 градусам, а $\varphi$1 $=$ 60 градусам.

Итак, решение:
АС $=$ AD $+$ DC.
AD $=$ htg$\varphi$1, DC $=$ htg$\varphi$2
Таким образом, АС $=$ h(tg$\varphi$1 $+$ tg$\varphi$2).
Одновременно с этим имеем: АС $=$ vaT и ВС $=$ vчT , где va и vч - это скорости автобуса и человека соответственно, а T , как уже было оговорено - время прибытия обоих на остановку С, одинаковое в обоих случаях.
Т.е. для имеем для автобуса
vaТ $= $ h(tg$\varphi$1 $+$ tg$\varphi$2),
для человека же имеем
vчТ $=$ BC,
или vчТ $= $ $\frac{h}{\cos\varphi2}$
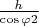
Но по условию vч $=$ $\frac{va}{\sqrt{2}}$.
Отсюда $\frac{va}{\sqrt{2}}$Т $= $ $\frac{h}{\cos\varphi2}$.
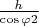
То есть, vaТ $=$ $\frac{\sqrt{2}h}{\cos\varphi2}$
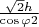
Приравнивая выражения для vaТ получаем, что h(tg$\varphi$1 $+$ tg$\varphi$2) $=$ $\frac{\sqrt{2}h}{\cos\varphi2}$.
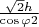
Сокращаем h, получаем
tg$\varphi$1 $+$ tg$\varphi$2 $=$ $\frac{\sqrt{2}}{\cos\varphi2}$.
По формуле суммы тангенсов, в которую подставляем значение $\varphi$1 $+$ $\varphi$2 $=$$\varphi$, получается, что
$\frac{\sin\varphi}{\cos\varphi1\cos\varphi2}$ $=$ $\frac{\sqrt{2}}{\cos\varphi2}$.
Сокращаем $\cos\varphi$2 и, с учётом найденного выше угла $\varphi$1=60 град приравнивая $\cos\varphi$1 $=$ $\frac{1}{2}$ получаем, что синус искомого угла фи равен $\frac{\sqrt{2}}{2}$, то есть угол $\varphi$ $= $ 45 градусам.
Т.е., абсурд.
Задачу, вероятно, можно решить теоремой синусов (кстати, применив и обозначенный на рис.1 угол $\alpha$), хотя пока опять же получается что-то невразумительное.
Между тем, ответ можно получить просто из соотношения $\frac{vч}{vа}$ $= $ $\frac{1}{\sqrt{2}}$, т.е. угол между векторами скоростей равен 45 градусов. Отсюда же получаем угол между сторонами треугольника AC и BC (расстояния, полученные умножением векторов соотв. скоростей на одно и то же время Т) и, наконец, угол $\varphi$2, который тоже равен 45 градусам. Прибавив который к первому подуглу $\varphi$1, который по условию равен 60 градусам, получаем искомое значение 105 градусов.
Я просмотрел решение с суммой тангенсов раз сто и не нашёл никакой ошибки. Но постоянно получаю в качестве ответа угол $\varphiфи$ равный углу, допустим, $\beta$ при вершине С $= $ 45 градусам.
Так где же ошибка? Или я неверно понял условие?

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неинформативный заголовок;
- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- условие задачи нужно написать в тексте сообщения, а не давать ссылку на весь задачник целиком.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.