Сложная задача по планиметрии

[Rusit8800]

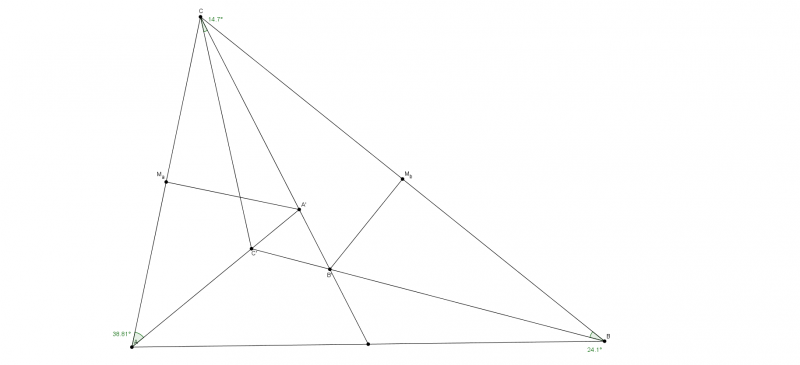
Пусть $CC_0$ - медиана в треугольнике $ABC$. Перпендикуляры к сторонам $AC$ и $BC$ из их середин $M_a$ и $M_b$ пересекают $CC_0$ в точках $A'$ и $B'$, прямые $AA'$ и $BB'$ пересекаются в точке $C'$. Докажите, что

$$\[\angle C'C{C_0} = \left| {\angle CAA' - \angle CBB'} \right|\]$$

Все, что мне удалось, это выразить углы треугольника $A'B'C'$ через углы $\[\angle CAA' = \alpha \]$ и $\[\angle CBB' = \beta \]$ через теорему о внешнем угле и о сумме углов треугольника. Также, мне удалось доказать с помощью тригонометрии, что углы $\alpha$ и $\beta$ однозначно задают вид треугольника $ABC$ (два угла, на которые медиана разделяет угол $C$), это значит, что теоретически можно подсчитать все углы в этом треугольнике(причем это верно не только для медианы, а для любой чевианы, если задано отношение, в котором она делит сторону). Но на практике этого сделать не удается: при счете углов у меня получается использовать только то, что $CC_0$ - чевиана треугольника, а то, что это конкретно медиана - нет. Если бы это была биссектриса или высота, то было бы проще считать углы, но что делать с медианами - я не знаю.

-- 22.06.2017, 19:54 --

[Munin]

Rusit8800 в сообщении #1228464 писал(а):

Все, что мне удалось, это выразить углы треугольника $A'B'C'$ через углы $\[\angle CAA' = \alpha \]$ и $\[\angle CBB' = \beta \]$

Ну и чему они равны?
Вы нашли правильный путь, но прошли только полдороги.

-- 22.06.2017 20:26:37 --

Смотреть на чертёж ужасно: буквы нечитаемо мелкие.

[arqady]

Там же два равнобедренных треугольника.

[Rusit8800]

arqady в сообщении #1228524 писал(а):

Там же два равнобедренных треугольника.

Вы не поверите, но это первое, что я обнаружил в констукции при задачи .

-- 23.06.2017, 10:09 --

Munin в сообщении #1228483 писал(а):

Ну и чему они равны?

$\[\angle A'B'C' = 2\beta \]$, $\[\angle C'A'B' = 2\alpha \]$

-- 23.06.2017, 10:12 --

Munin в сообщении #1228483 писал(а):

Вы нашли правильный путь, но прошли только полдороги.

Значение углов $\[\angle A'B'C'\]$ и $\[\angle C'A'B'\]$ верно для любой чевианы $CC_0$, а вот воспользоваться тем, что $CC_0$ - медиана я не могу: нельзя без тригонометрии посчитать углы, связанные с ней.

-- 23.06.2017, 10:16 --

[wrest]

Rusit8800
Попробуйте найти соотношение между углами $\angle C'CA$ и $\angle B'CB$

[Rusit8800]

wrest в сообщении #1228720 писал(а):

Попробуйте найти соотношение между углами $\angle C'CA$ и $\angle B'CB$

Из задачи следовало бы, что $CC_0$ - симедиана, следовательно $\angle C'CA = \angle B'CB$. Я пытался это доказать, так как отсюда следует и условие задачи, но доказать это никак не удается.

-- 23.06.2017, 12:49 --

Знал бы я $\angle C'CB$.

[Munin]

Rusit8800 в сообщении #1228703 писал(а):

$\[\angle A'B'C' = 2\beta \]$, $\[\angle C'A'B' = 2\alpha \]$

Прямая подсказка: и чему в таком случае равен $\angle B'C'A'$?

[wrest]

Rusit8800 в сообщении #1228754 писал(а):

Из задачи следовало бы, что $CC_0$ - симедиана,

Да, по сути вам как раз и надо доказать что отрезок $CC'$ (!! а не $CC_0$) - принадлежит симедиане треугольника $ABC$, проведенной из его вершины $C$

[wrest]

Rusit8800
Опустите перпендикуляры из $A$ и $B$ на медиану $CC_0$
Что можете сказать об их длине? В этом умозаключении используется как-то то, что $CC_0$ медиана?

[Rusit8800]

Munin в сообщении #1228777 писал(а):

чему в таком случае равен $\angle B'C'A'$?

Ну $\[180 - 2\alpha - 2\beta \]$

wrest в сообщении #1228819 писал(а):

а не $CC_0$

Ну да.

wrest в сообщении #1228875 писал(а):

Что можете сказать об их длине? В этом умозаключении используется как-то то, что $CC_0$ медиана?

Ну равны они по гипотенузе и острому углу.

[wrest]

Rusit8800 в сообщении #1228883 писал(а):

Ну равны они по гипотенузе и острому углу.

А что можете сказать о длине перпендикуляров опущенных из $C$ на $AA'$ и $BB'$?

[Munin]

Rusit8800 в сообщении #1228883 писал(а):

Ну $\[180 - 2\alpha - 2\beta \]$

Это было не "ну", а подсказкой, куда копать дальше.

Я не намерен решать задачу целиком за вас.

[Rusit8800]

Munin в сообщении #1228920 писал(а):

Это было не "ну", а подсказкой, куда копать дальше.

За первые десять минут я нашел значение этого угла, а остальные 3 часа копал.

[Munin]

Задача нубанальная же. Рассмотрите теперь другой треугольник...

[wrest]

Munin в сообщении #1228932 писал(а):

Задача нубанальная же.

Вполне олимпиадная, кстати.