Объясните квантовые вычисления

Xaositect · 06/10/08 6422

Если говорить конкретно про алгоритм факторизации Шора, то там на входе система без запутывания, ее можно получить просто установкой каждого кубита в нужное состояние.
Проблемы могут быть с тем, что сильно запутанные состояния из-за шума могут быстро становиться бесполезными, об этом пишет Gil Kalai.

AlexNew · 28/06/08 1706

george66 писал(а):

Возьмём для примера 50 кубитов. Пространство состояний имеет размерность $2^{50}$ (тензорное произведение 50 двумерных пространств)...
Мы делаем линейные операции над одним-двумя кубитами за раз, получаем вектор в пространстве $2^{50}$ .

Чтобы получить тензорное произведение надо наверное эти кубиты как то за запутать, это уже будут не кубиты а совсем другое слово слово.
Собственный базис токай системы будет $2^{50}$ базисных векторов, значит ответ будет тоже $2^{50}$ чисел.

george66 писал(а):

Выбираем базис (произвольный), измеряем состояние системы и вместо вектора размерности $2^{50}$ получаем один из векторов базиса.

Вот что меня беспокоит:
1) мы вектор малого числа измерений (исходные данные которые вводим) превращаем в вектор огромного числа измерении, поворачиваем его и опять превращаем его в вектор малого числа измерений (то что мы можем измерять после многих экспериментов). Так ?
(Если можно так пошутить, это как если бы у нас было число, мы дописали кучу нулей после запятой, в операциях соблюдали всю эту точность а в конце опять округлили

)

2) Тензорное произведение кубитов,
Если вы просто поставите кубиты или гейты друг за дружкой никакого тензорного произведения не будет!
Должна быть система у которой будут, в нашем случае $2^{50}$ , линейно независимых собственных базисных векторов!
Как это сделать?

Xaositect писал(а):

Если говорить конкретно про алгоритм факторизации Шора, то там на входе система без запутывания, ее можно получить просто установкой каждого кубита в нужное состояние.

Получается в таком случает нет тензорного произведения, и я могу это посчитать на своем телеф... компьютере!

Xaositect · 06/10/08 6422

Кубиту соответсвует двумерное пространство, любой кубит находится в суперпозиции $\alpha \left|0\right> + \beta \left|1\right>$ . Если у нас система состоит из нескольких частей, то состояния системы - это тензорные произведения состояний частей. Например, система из 2 кубитов будет соответствовать четырехмерное пространство $\alpha \left|0\right>\otimes \left|0\right> + \beta \left|0\right>\otimes \left|1\right> + \gamma \left|1\right>\otimes \left|0\right> + \delta \left|1\right>\otimes \left|1\right>$ . Обычно пишут сокращенно, без знака тензорного произведения, напр. $\left|01\right> = \left|0\right>\otimes \left|1\right>$ . Для 50 кубитов будет $2^{50}$ , возможный базис состоит из всех комбинаций $\left|a_1 a_2 \dots a_{50}\right>$ , в которых каждый кубит находится в состоянии $\left|0\right>$ или $\left|1\right>$ .

Состояния бывают разложимые, например $\left|00\right> = \left|0\right> \otimes \left|0\right>$ или $(\left|00\right> + \left|01\right> + \left|10\right> + \left|11\right>) = (\left|0\right> + \left|1\right>)\otimes(\left|0\right> + \left|1\right>)$ , где два кубита находятся каждый независимо в своем состоянии, и запутанные, напр. $\left|00\right> + \left|11\right>$ , где будут корреляции между измерениями.

В квантовых алгоритмах обычно на вход подается разложимое состояние вида $\left|a_1 a_2 \dots a_{n}\right>$ , в котором каждый кубит имеет конкретное состояние из выбранного базиса и не спутан с другими. Готовить такие состояния просто. И на выходе после измерения (в соответствующем базисе) получается тоже такое состояние. А вот в процессе работы алгоритма могут использоваться все возможные спутанные состояния из $2^n$ -мерного пространства.

AlexNew · 28/06/08 1706

Не понятно,..

1. Давайте предположим у нас есть 2 независимые системы:
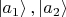
2х уровненная система $A$ с 2мя собственными функциями/состояниями $\left|a_1\right>,\left|a_2\right>$ и собств. знач. $\alpha_1, \alpha_2$ .
3х уровненная система $B$ с 3мя собственными функциями/состояниями $\left|b_1\right>,\left| b_2\right>, \left|b_3\right>$ и собств. знач. $\beta_1, \beta_2, \beta_3$ .

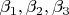
(Нам нужно 3 уровня для изложения проблемы наиболее кратко.)
Мы знаем как проводить измерения и получать наши собственные значения.

2. Теперь чудесным образом мы сделали из 2х систем одну (как?)
Теперь у нас $2 \otimes 3 = 6$ собственных функции $\left|a_1 b_1\right>, \left|a_1 b_2\right>, \left|a_1 b_3\right>, \left|a_2 b_1\right>, \left|a_2 b_2\right>, \left|a_2 b_3\right>$ и, соответственно, $6$ собственных значений, а было то всего $5$ , появилась новая!

Чтобы такое чудо произошло очевидно нужен новый оператор в который войдет некая константа связи между двумя нашими системами.
У которого будут свои отличные собственные значения и функции. Да, они будут отличными и их станет на одну больше в нашем случае.

С кубитами будет та же беда.
Да, у нас быстро возрастает количество собственных состояний как ~ 2^Ν но ценой усложнения физики/оператора, появления всяких констант связи, новых собственных значений которые не понятно как измерять.

Не улавливаю смысл.

-- Вс июл 30, 2017 05:32:00 --

Xaositect писал(а):

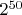
напр. $\left|01\right> = \left|0\right>\otimes \left|1\right>$ . Для 50 кубитов будет $2^{50}$ , возможный базис состоит из всех комбинаций $\left|a_1 a_2 \dots a_{50}\right>$ , в которых каждый кубит находится в состоянии $\left|0\right>$ или $\left|1\right>$ .

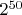
То есть в данном случае я хочу сказать что $\left|01\right> = \left|0\right>\otimes \left|1\right>$ это совсем отличное от $\left|0\right>$ и $\left|1\right>$ не понятное состояние которое не ясно как измерять и которому соответствует непонятное собственное значение, и этих непонятных состояний $2^{50}$ штук.
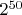
В результате измерения мы будем получать одно из $2^{50}$ чисел.
Очевидно все эти числа будут лежать очень плотненько, и отличить эти числа/отгадать в каком состоянии находится система будет очень не просто даже после громадного числа измерений. Перепутаете 2.23456345 с 2.23456347 в эксперименте и примите за решение совсем другое состояние, бесконечно далекое от верного ответа.

Не понятно!

george66 · 31/12/15 922

Лично мне помогла вероятностная аналогия. Возьмём 50 обычных битов, получим $2^{50}$ возможных комбинаций. Если на пространстве состояний задано распределение вероятностей, это будет $2^{50}$ действительных чисел (вероятностей). Среди всех распределений вероятностей есть небольшое подмножество разложимых, которые делаются так: задаём вероятности $p_1, p_2, p_3\ldots p_{50}$ того, что наши биты принимают значение 1 (для каждого бита своё число), тогда вероятности всех $2^{50}$ комбинаций легко вычисляются. Далеко не все распределения вероятностей разложимы! Для разложимого надо задать 50 чисел, а для произвольного $2^{50}$ ! В квантовой механике вместо вероятностей комплексные числа (амплитуды), но в остальном всё то же самое. Задаём исходные 50 чисел $p_1,p_2,p_3\ldots p_{50}$ . Проделываем над битам какие-то вычисления, получаем один из $2^{50}$ возможных ответов, вероятности их легко вычислить. А затем фокус: проводим такое измерение, что ответ будет зависеть от всех $2^{50}$ возможных результатов (классически это невозможно). Для этого выбираем в пространстве состояний произвольный базис (формально это $2^{50}$ векторов, но реально чисел надо гораздо меньше, поскольку вектора берём разложимые)

arseniiv · 27/04/09 28128

(Оффтоп)

«Нет, всё равно не понятно!»

maximav · 19/03/15 291

george66 в сообщении #1236820 писал(а):

Лично мне помогла вероятностная аналогия.

Я бы заметил, что как раз вероятностная и путает мозг и вряд ли что объяснит. Не помню где, в этой ветке или другой, я писал, что вовлечение вероятности даже хуже, чем математические аналогии. Она принципиально не физична. А "естественный" переход

george66 в сообщении #1236820 писал(а):

В квантовой механике вместо вероятностей комплексные числа (амплитуды)

вообще, настолько туманный, что искать здесь прояснение безнадежно. Какие еще такие амплитуды?

arseniiv · 27/04/09 28128

maximav в сообщении #1237014 писал(а):

Я бы заметил, что как раз вероятностная и путает мозг и вряд ли что объяснит. Не помню где, в этой ветке или другой, я писал, что вовлечение вероятности даже хуже, чем математические аналогии. Она принципиально не физична.

Кому как кажется. По-моему, вероятность — очень хорошее подспорье, особенно когда обобщается до некоммутативной. Аналогии вылезают сами собой в больших количествах. А лучшее — враг хорошего (если оно притом действительно лучшее, хе).

maximav · 19/03/15 291

А где вы в физической эмпирике наблюдаете такую сущность, как вероятность? Математически она аксиоматизирована, но причем здесь физические наблюдения? И причем здесь, в том числе и в КМ, некоммутативность? А предложения

arseniiv в сообщении #1237021 писал(а):

А лучшее — враг хорошего (если оно притом действительно лучшее, хе).

я, честно говоря, просто не понял. Хорошее в КМ то, что все замечательно работает и не найдено ни единой контры. А плохое в том, что не понятно откуда берется вся такая экзотика, как КМ. Но именно на ее интерпретациях и воздвигается здание квантовых вычислений.

arseniiv · 27/04/09 28128