Дан интервал. В Вашей статье проводится оценка максимальной длины прогрессии, возможных знаменателей.
Только вот нюанс в том ,что это интервал по мере роста оценки
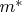
сокращается, верхняя граница тоже сокращается не хуже корня (неизвестной степени) -
вот вопрос в том как оценить сокращение.. Да и нижняя растет , что сокращает перебор.
Цитата:
А дальше начинаем считать.
В псевдокоде у Вас одни процедуры. Где программа-то?
Цитата:
Дык первая процедура и есть программа - на входе

- на выходе

. Логарифмы -корни имеют сложность пропорциональную длине(условно говоря найти делением максимальную степень, либо перебором по разрядам корень)
Давайте возьмём "взрослый" интервал
![$[10^9, 6 \cdot 10^9]$ $[10^9, 6 \cdot 10^9]$](https://dxdy-03.korotkov.co.uk/f/6/1/e/61e3da537c69dfc877def223eaa2729582.png)
.
Как происходит проверка конкретного знаменателя? - Я к чему? Вы утверждаете, что алгоритм у Вас "экспоненциальный".
Потому что верхняя граница , как мне кажется ( о чем и стоит вопрос) и останется функцией намного большего роста, чем логарифм верхней границы ака длины верхней границы...
Цитата:
Т.е. кроме сканирования по всему (или его конечной части) интервалу для определения первого члена не видно.
А значит, время счёта тупо пропорциональна длине интервала. И никакой экспоненты.
Ну думать или спрашивать об оптимизации никому не запрещено...Тем более есть такая вещь в музыке - называется октава...Там ведь для практических целей создания музыкальных инструментов аппроксимируют

ближайшими цепными дробями....вот и думаю нельзя ли как -то и здесь применить цепные дроби для сокращения поиска - их числители знаменатели ведь тоже растут экспоненциально с каждым шагом аппроксимации