Вот это не очень похоже на нормальное доказательство.
Можно написать это более длинно как «

является элементом
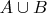
тогда и только тогда, когда он является элементом

или [он является элементом]

», хотя проще будет записать то же самое в виде

.
Допустим, известна только логика высказываний.
Тогда не получится. А определениях пустого множества и объединения существенно используется первопорядковость языка теории множеств. В самом деле, это же предметные константа и бинарная операция, такого в языке высказываний просто нет.