Задача: Дан выпуклый многоугольник площади

. Его пересекают

параллельных прямых на расстоянии

друг от друга. Докажите, что сумма длин отрезков, высеченных многоугольников на этих прямых, не более десяти.
Она уже встречалась
здесь. В процессе решения, я обнаружил, что искомая экстремальная конфигурация должна обладать следующим свойством: ее опорными прямыми являются "крайние" прямые

и

. Действительно, если найдется какой-то "торчащий кусок", то его всегда можно отрезать, преобразовать так, чтобы его можно было наложить так, чтобы он лежал внутри

и

, и чтобы он пересекал хотя бы одну из этих параллельных прямых(естественно, такое преобразование должно сохранить "выпуклость" исходной конфигурации). Отсюда следует, что конфигурация с "торчащими кусками" не является экстремальной, её можно не рассматривать. Далее возникли проблемы с поиском такой конфигурации. А все из-за того, что площади

"недостаточно" (вот если бы была площадь

, было бы другое дело). У меня получились конфигурации, сумма высекаемых этими конфигурациями отрезков которых равна

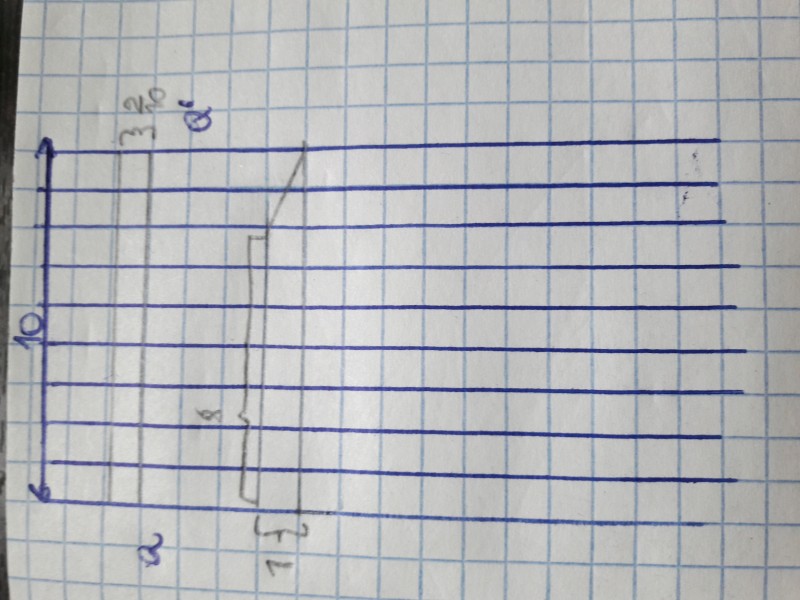
: прямоугольник стороной

и трапеция высотой

. Такие же конфигурации были предложены ТС той
темы.