Макрообъект с точностью до микрочастиц

[madschumacher]

Formalizator в сообщении #1186001 писал(а):

извлечь классическое описание системы.

По-моему тут что-то намешано. Как из квантового описания получить классическое описание системы -- это другая задача, она решается как в рамках квант.меха (уже много раз тут обсуждалось), так и в рамках квантового стат.меха (например, банальный переход от Ферми-Дирака к Максвеллу-Больцману). В обоих случаях идея одна и та же, но вопрос и способ решения несколько другой.

Если же Вас интересуют именно макросвойства кристаллов/жидкостей/газов (типа давления, температуры, плотности, скорости звука и т.д.), то Вам нужно смотреть на стат.мех. в чистом виде (причём, концептуально не важно, имхо, классический он будет или квантовый).

[Munin]

madschumacher
Окститесь. Скорость звука в кристалле существенно квантового происхождения.

[Kamaz]

Munin в сообщении #1186076 писал(а):

Скорость звука в кристалле существенно квантового происхождения.

Выражение для скорости волн на струне не содержит постоянной Планка. Что Вы имели в виду под "квантовостью происхождения"?

[madschumacher]

Munin в сообщении #1186076 писал(а):

Скорость звука в кристалле существенно квантового происхождения.

Ну так я про газ в т.ч. говорил. Естественно, там могут быть тонкости в разных вопросах (я же не предлагаю сверхтекучесть из классического стат.меха выводить )

[Munin]

Kamaz в сообщении #1186095 писал(а):

Что Вы имели в виду под "квантовостью происхождения"?

Дисперсионное соотношение для фононов. Впрочем, да, вы правы. Но и я прав: закон Гука происходит из квантового закона межатомного потенциала! Из кваратичной аппроксимации дна ямки в этом потенциале.

[Formalizator]

Formalizator в сообщении #1186001 писал(а):

Вопрос в том, каким образом из этих функций извлечь классическое описание системы.

Munin в сообщении #1186017 писал(а):

Открыть учебник.

Имеется: Л. Д. Фаддеев, О. А. Якубовский "Лекции по квантовой механике для студентов-математиков".

В этой книге приведено определение квантового состояния (§ 6) и рассмотрен переход от квантовой механики к классической (§ 14). Делается следующий вывод:

Цитата:

чистому состоянию квантовой механики при $\hbar \to 0$ может соответствовать смешанное классическое состояние.

[Munin]

Не этот учебник. А уже названные вам по ФТТ.

[Formalizator]

Имеется ли теоретическое обоснование способности атомных ядер и электронов образовывать твёрдые тела? (Твёрдое тело может быть кристаллическим или аморфным.)

Т.е. почему электроны удерживают атомные ядра вместе, так что расстояния между соседними ядрами находятся в небольших пределах?

Этот вопрос затронут в главе 20 "Когезионная энергия" книги Н.Ашкрофт, Н.Мермин "Физика твёрдого тела", но рассматривается там не фундаментально.

И каким образом описывать движение ядер и электронов в твёрдом теле? Классическая кинематика не годится. Волновая функция? Но это же у нас макрообъект, принцип суперпозиции в полной мере не действует. Тогда что?

[madschumacher]

Formalizator в сообщении #1206377 писал(а):

Т.е. почему электроны удерживают атомные ядра вместе, так что расстояния между соседними ядрами находятся в небольших пределах?

А по-Вашему есть разница этих сил в ТТ от тех, что держат вместе атомы в молекулах газов и жидкостей, а также сами эти молекулы вместе в жидкостях?
Спойлер: её (разницы) нет.
А разница возникает в "навороченности" формул. Впрочем, кристалл может оказаться и проще для описания, чем его же расплав...

Formalizator в сообщении #1206377 писал(а):

Волновая функция?

Да, именно ВФ. Ну или матрица плотности (или даже её одноэлектронный след, a.k.a. электронная плотность). У КМ есть не единственный взгляд на вещи.

(а можно и так)

Можно, в принципе, на электроны с помощью классической кинематики смотреть через призму фейнмановских интегралов по траекториям, даже обойтись уравнениями Ньютона, с некоторой "модификацией действующих сил" (из-за взаимодействия траекторий), а при температурах больше 0 К, так даже конечным числом траекторий. Но суть КМ от этого не изменится.

Formalizator в сообщении #1206377 писал(а):

Но это же у нас макрообъект, принцип суперпозиции в полной мере не действует.

Кто Вам такую ерунду сказал?

[Formalizator]

madschumacher в сообщении #1206379 писал(а):

Formalizator в сообщении #1206377 писал(а):

Т.е. почему электроны удерживают атомные ядра вместе, так что расстояния между соседними ядрами находятся в небольших пределах?

А по-Вашему есть разница этих сил в ТТ от тех, что держат вместе атомы в молекулах газов и жидкостей, а также сами эти молекулы вместе в жидкостях?

Строение атомов, химические связи, строение молекул и взаимодействие молекул нужно теоретически предсказать.
Про силы я ничего не говорил. Я говорил про атомные ядра и электроны. Имеются определённые законы поведения этих частиц. Эти законы и обеспечивают возможность существования атомов, молекул, жидкостей и твёрдых тел.

madschumacher в сообщении #1206379 писал(а):

Да, именно ВФ. Ну или матрица плотности (или даже её одноэлектронный след, a.k.a. электронная плотность). У КМ есть не единственный взгляд на вещи.

Определённое квантовое состояние определённого класса квантовых систем (чистое или смешанное - не важно) однозначно сопоставляет каждой квантовой наблюдаемой того же класса квантовых систем определённое вероятностное распределение по возможным результатам измерения этой наблюдаемой.

Другими словами, для каждого класса квантовых систем существует единственная однозначная функция двух аргументов, первый аргумент - квантовое состояние систем этого класса, второй аргумент - квантовая наблюдаемая систем этого класса, значение - вероятностное распределение по результатам измерения указанной наблюдаемой.

Смысл понятия "квантовое состояние" заключается именно в этом.

madschumacher в сообщении #1206379 писал(а):

Formalizator в сообщении #1206377 писал(а):

Но это же у нас макрообъект, принцип суперпозиции в полной мере не действует.

Кто Вам такую ерунду сказал?

Карандаш не может находиться в состоянии суперпозиции сильно различных положений в пространстве.

[Munin]

Да, базовую квантовую механику всё-таки надо знать. ЛЛ-3 § 32.

[madschumacher]

Formalizator в сообщении #1206608 писал(а):

Строение атомов, химические связи, строение молекул и взаимодействие молекул нужно теоретически предсказать.

..что успешно делается, начиная с 30-х годов XX-го века... Твёрдые тела тут не исключение.

Formalizator в сообщении #1206608 писал(а):

Про силы я ничего не говорил.

Силы -- это образное выражение. В данном контексте они обозначали химические связи любого рода (т.е. ковалентные, ионные, металлические), а также межмолекулярные взаимодействия между различными частицами (и молекулярные кристаллы, уж простите, бывают).

Formalizator в сообщении #1206608 писал(а):

Я говорил про атомные ядра и электроны.

А я, видимо, про крокодилов и пирамиды.

Formalizator в сообщении #1206608 писал(а):

Имеются определённые законы поведения этих частиц. Эти законы и обеспечивают возможность существования атомов, молекул, жидкостей и твёрдых тел.

... и имя им квантовая механика и электромагнетизм... что конкретно не то я сказал по-Вашему?

Formalizator в сообщении #1206608 писал(а):

madschumacher в сообщении #1206379 писал(а):

Formalizator в сообщении #1206377 писал(а):

Но это же у нас макрообъект, принцип суперпозиции в полной мере не действует.

Кто Вам такую ерунду сказал?

Карандаш не может находиться в состоянии суперпозиции сильно различных положений в пространстве.

Т.е. это Вам сообщил карандаш, который не может что-то там делать? Вы можете чётко сформулировать принцип суперпозиции, или нет?

(hint)

на языке формул это делать проще, чем с использованием естественного языка...

Formalizator в сообщении #1206608 писал(а):

Определённое квантовое состояние определённого класса квантовых систем (чистое или смешанное - не важно) однозначно сопоставляет каждой квантовой наблюдаемой того же класса квантовых систем определённое вероятностное распределение по возможным результатам измерения этой наблюдаемой.

Другими словами, для каждого класса квантовых систем существует единственная однозначная функция двух аргументов, первый аргумент - квантовое состояние систем этого класса, второй аргумент - квантовая наблюдаемая систем этого класса, значение - вероятностное распределение по результатам измерения указанной наблюдаемой.

Если много раз употребить слово "квантовый" без всякой необходимости, то можно вызвать:

• Битлджуса Munin-а, указывающего на необходимость чтения учебников,
• недоумение у читающего.

Вы добились и того и другого.
Если продраться через дебри написанного, то кажется, что Вы написали что-то похожее на правду (хоть и очень заумно). Но остаётся непонятным зачем Вы это всё написали, и что конкретно Вы хотели этим сказать?

[arseniiv]

Formalizator в сообщении #1206608 писал(а):

Карандаш не может находиться в состоянии суперпозиции сильно различных положений в пространстве.

Почему же не может — может, просто крайне недолго. Если его хорошенько заморозить и засунуть в вакуум — может быть, подольше продержится.

[Formalizator]

Munin в сообщении #1206614 писал(а):

Да, базовую квантовую механику всё-таки надо знать. ЛЛ-3 § 32.

В контексте данной темы это к атому водорода, двухатомной молекуле, или к чему?
В формализме квантовой механики, когда задача поставлена, решить её - чисто технический вопрос.

madschumacher в сообщении #1206641 писал(а):

Formalizator в сообщении #1206608 писал(а):

Строение атомов, химические связи, строение молекул и взаимодействие молекул нужно теоретически предсказать.

..что успешно делается, начиная с 30-х годов XX-го века... Твёрдые тела тут не исключение.

Да, квантовохимические расчёты проводят. Но вопрос был - вывести, что из атомных ядер и электронов получается твёрдое тело. А характерное свойство твёрдого тела - обладание определённой геометрической формой, определённым положением в пространстве в каждый момент времени. Именно это должно быть предсказано теоретически.

(Геометрическая форма и время)

Жидкость тоже в каждый момент времени обладает определённой геометрической формой и определённым положением в пространстве. У твёрдого тела геометрическая форма довольна стабильна (с течением времени обычно практически не меняется), а у жидкости нестабильна (с течением времени легко меняется). Твёрдое тело при внешних воздействиях подвергается практически обратимым упругим деформациям, может разделяться на части с образованием новых поверхностей. Ещё бывают пластичные тела, эластичные тела...

А в квантовохимических расчётах атомные ядра обычно рассматривают классически, разве нет?

(Квантовое рассмотрение движения атомных ядер)

Ну ещё бывают вибронные состояния...

madschumacher в сообщении #1206641 писал(а):

Formalizator в сообщении #1206608 писал(а):

Карандаш не может находиться в состоянии суперпозиции сильно различных положений в пространстве.

Т.е. это Вам сообщил карандаш, который не может что-то там делать? Вы можете чётко сформулировать принцип суперпозиции, или нет?

(Вспомогательное, но необходимое пояснение)

Ненулевому кет-вектору $|\psi\rangle$ сопоставляется состояние $\hat\rho$ по формуле

$$ \hat\rho = \frac{|\psi\rangle\langle\psi|}{\langle\psi|\psi\rangle} $$

В таком случае будем называть $\hat\rho$ "состояние с кет-вектором $|\psi\rangle$". Разумеется, $|\psi\rangle$ не может быть нулевым.

Принцип суперпозиции: пусть возможны состояние с кет-вектором $|\psi_1\rangle$ и состояние с кет-вектором $|\psi_2\rangle$. Тогда для любых ненулевых комплексных чисел $c_1$ и $c_2$ возможно состояние с кет-вектором $|\psi\rangle = c_1|\psi_1\rangle + c_2|\psi_2\rangle$.

madschumacher в сообщении #1206641 писал(а):

Но остаётся непонятным зачем Вы это всё написали, и что конкретно Вы хотели этим сказать?

Чтобы привести смысл понятия "квантовое состояние". Можно проще:

Каждой упорядоченной паре (квантовое состояние, квантовая наблюдаемая) однозначно соответствует вероятностное распределение по возможным результатам измерения указанной наблюдаемой.

-- 06.04.2017, 02:32 --

arseniiv в сообщении #1206687 писал(а):

Formalizator в сообщении #1206608 писал(а):

Карандаш не может находиться в состоянии суперпозиции сильно различных положений в пространстве.

Почему же не может — может, просто крайне недолго. Если его хорошенько заморозить и засунуть в вакуум — может быть, подольше продержится.

Каким образом наблюдать суперпозицию сильно различных положений одного и того же объекта?

[madschumacher]

Formalizator в сообщении #1206860 писал(а):

Но вопрос был - вывести, что из атомных ядер и электронов получается твёрдое тело.

Ну а в чём проблема то? Для расчёта свойств кристалла необходимо посчитать элементарную ячейку (ЭЯ), или же суперячейку. Оттуда можно прикинуть электронные свойства, да даже фононные спектры уже пытаются моделировать, см. тут или тут, например (правда, там не совсем квантовой химией пользуются, а молекулярно-механическими силовыми полями $+$ классической молдинамикой, но имхо разницы не особо много ).
Для кристалла Вы находите стабильную конфигурацию ядер в элементарной ячейке (относительно смещений ядер), и зная её Вы понимаете, что из сингонии Вы уже фактически знаете макроскопическую форму кристалла. Фсё.

Formalizator в сообщении #1206860 писал(а):

Именно это должно быть предсказано теоретически.

На эту тему можете на Postnauka посмотреть ролики Артёма Оганова.

Formalizator в сообщении #1206860 писал(а):

Твёрдое тело при внешних воздействиях подвергается практически обратимым упругим деформациям, может разделяться на части с образованием новых поверхностей. Ещё бывают пластичные тела, эластичные тела...

Ну это уже более макроскопические эффекты, ну свойственные не только кристаллам, а каким-нть некристаллическим полимерам. Молдинамикой с силовыми полями всякие упругие свойства (в т.ч. и разрыв) уже моделируют.

Formalizator в сообщении #1206860 писал(а):

А в квантовохимических расчётах атомные ядра обычно рассматривают классически, разве нет?

Нет. В квантово-химических расчётах обычно используют приближение Борна-Оппенгеймера, поэтому ядра тупо являются "замороженными", т.е. создают поле, в котором движутся электроны. Если же рассматривают движения ядер в поле электронов (ну или совместное их движение), то когда рассматривают ядра классической механикой об этом пишут в явном виде, и называется это "классическая молекулярная динамика".
А есть ещё квантовая молдинамика, основанная на фейнмановских интегралах по траекториям.
Но для малых молекул (до 100 атомов) обычно используют только квантовые модели в явном виде. А классическую молдинамику уже гоняют для систем с числом атомов $10^2 - 10^6$.

Formalizator в сообщении #1206860 писал(а):

Ну ещё бывают вибронные состояния...

Вообще-то даже вращения и колебания в молекулах -- это весьма квантовые явления. С точки зрения классической механики рассматривать экспериментальный вращательный (микроволновый диапазон) или колебательно-вращательный спектр молекулы (инфракрасный диапазон) -- это заведомо тупиковая идея.

Formalizator в сообщении #1206860 писал(а):

Принцип суперпозиции

Ок.

Formalizator в сообщении #1206860 писал(а):

Каждой упорядоченной паре (квантовое состояние, квантовая наблюдаемая) однозначно соответствует вероятностное распределение по возможным результатам измерения указанной наблюдаемой.

ну допустим.

Formalizator в сообщении #1206860 писал(а):

Каким образом наблюдать суперпозицию сильно различных положений одного и того же объекта?

А Вы попробуйте для разнообразия оценить порядок квантовых эффектов для карандаша.
Возьмите, например, для определённости знаменитые карандаши из IKEA.

(фото)

В Вики сказано, что их размер $7 \times 87$ мм. Аппроксимируем их прямоугольным параллелепипедом с гранями $7 \times 7 \times 87$ мм (объём $V=4.3 \ \text{см}^3$ ). Примем, что карандаши сделаны из ели ($\rho = 0.45 \ \text{г/см}^3$). Тогды, масса карандаша $m_\mathrm{pencil} \approx 2$ грамма.
Сделаем классические оценки. Пусть мы измеряем положение карандаша с точностью 1 мкм. Тогда по соотношению неопределённости $\delta x \cdot \delta p \geq \frac{\hbar}{2}$ мы получим, что оценка на погрешность измерения скорости $\delta v = \frac{\delta p}{m_\mathrm{pencil}} \geq \frac{\hbar}{2 m_\mathrm{pencil} \delta x} = 1.7 \cdot 10^{-25} $ м/c.

(график)

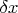
а если $\delta x$ варьировать вплоть до 1 м получим следующие минимальные $\delta v$:

А теперь давайте представим себе карандаш в виде гауссовского волнового пакета вдоль одной из координат $p(x) \propto \exp \left( - \frac{x^2}{\sigma^2} \right)$, где $\sigma$ -- ширина волнового пакета. Гауссовский пакет расплывается во времени, его ширина в момент $t$ становится $\sigma(t) = \sqrt{\frac{\sigma_0^4 + \left(\frac{\hbar t}{m_\mathrm{pencil}} \right)}{\sigma_0^2}}$, где $\sigma(0)=\sigma_0$.
Давайте примем, что в начальный момент времени $\sigma_0$ равна максимальной длине карандаша (8.7 см). Тогда его расплывание во времени будет выглядеть так:

то бишь, нифига он не расплывается!! за $10^{20}$ лет его ширина изменится всего на 0.08 см!!!!

Ну и Вы правда ожидаете при таких оценках какого-то квантового поведения от карандаша???