При положительных (a;b),

доказать неравенство
![$(4b^3+8b^2-11b)+(4a^3+8a^2-11a)+19ab^2+19a^2b+8ab\ge8[(a+b)^2-1]\sqrt{2ab+a+b}$ $(4b^3+8b^2-11b)+(4a^3+8a^2-11a)+19ab^2+19a^2b+8ab\ge8[(a+b)^2-1]\sqrt{2ab+a+b}$](https://dxdy-03.korotkov.co.uk/f/2/6/2/262e6b42e8f17225aeb4989b1fdb020882.png)
При этих условиях правая и левая части неотрицательны. Возведём их в квадрат. получим многочлен шестой степени, который при

неотрицателен, т.к. все его коэффициенты будут положительны при заданных условиях. Этот случай пропустим. Остаётся рассмотреть

.
В этом случае, после возведения в квадрат, представляем многочлен в виде суммы двух функций, выделяя с правого конца квадратный трёхчлен (кстати, у него отрицательный дискриминант). Смотрим на знак коэффициента при старшей степени квадратного трёхчлена, и получаем точку, с которой надо начать исследование. Далее получаем новую точку, рассматривая

. Оставшийся промежуток исследуется стандартно с помощью производной и учёта свойства функции, имеющей один действительный корень на промежутке (т.е. её достаточно исследовать на концах промежутка для выяснения сохранности её знака на этом промежутке).
Остаётся проверить арифметику.
![$f=[16a^6+(136ab+56)a^5+(449b^2+328b-24)a^4+(658b^3+592b^2-346b-160)a^3]_1+[(449b^4+592b^3-580b^2-304b+121)a^2+(136b^5+328b^4-346b^3-304b^2+226b-8)a+(16b^6+56b^5-24b^4-160b^3+121b^2-8b)]_2$ $f=[16a^6+(136ab+56)a^5+(449b^2+328b-24)a^4+(658b^3+592b^2-346b-160)a^3]_1+[(449b^4+592b^3-580b^2-304b+121)a^2+(136b^5+328b^4-346b^3-304b^2+226b-8)a+(16b^6+56b^5-24b^4-160b^3+121b^2-8b)]_2$](https://dxdy-01.korotkov.co.uk/f/c/c/c/ccc8547d60eb4fafe665bcd6d6e4d43c82.png)









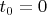

1).

Здесь дискриминант второй скобки отрицателен. Старший коэффициент положителен. Первая скобка положительна. Многочлен положителен.
2).

Количество положительных корней в обеих скобках не более одного. Берём минимум первой скобки при

и максимум второй скобки при

. Получаем

. Т.е.

.
3).

Здесь

имеет не более одного положительного корня.

, значит

. Т.е. сама функция монотонно возрастает и достаточно исследовать на концах промежутка

.
4).

Здесь дополнительно рассматриваем вторую и третью частные производные. Проблем не возникает. Всё сходится.
Конечно решение (если нет опечаток) громоздкое. Но было интересно убедится самостоятельно, что гипотеза "о следовании из непрерывно ложного во всей области определения" подтверждается стандартными методами.
(Оффтоп)
Гипотеза и не могла не подтвердится, т.к. при дополнительных условиях она элементарно доказывается. Поэтому она всегда подтверждается стандартными методами. Мне, по крайней мере, контрпримеры не встречались.