У уравнения
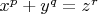
в натуральных числах при взаимно простых основаниях есть две гипотезы, дополняющие друг друга.
Гипотеза Биля говорит об отсутствии решений при всех степенях не ниже куба.
Гипотеза Ферма-Каталана говорит, что при выполнении условия
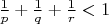
, то есть при одном квадрате в степени, система имеет конечное число решений, которые нужно найти.
По ссылке в стартовом сообщении дана таблица вариантов степеней, которые полностью рассмотрены, то есть все потенциальные корни при этих степенях найдены. Среди прочих указаны варианты степеней

равные

и

. Первый из них описывает случай гипотезы Биля для двух биквадратов при
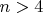
по неравенству на степени у Ферма-Каталана, а второй даёт случай при

.
Таким образом случай двух биквадратов гипотезы Биля полностью описывается. Но это утверждение верно лишь в том случае, если в таблице даны варианты с учётом возможных перестановок показателей степеней. Они там все в порядке возрастания, подозрительно. Поэтому и вопрос.
Учитывается ли в таблице перестановка степеней или нет?
Если не учитывается, то первый из приведённых вариантов не работает при разности двух биквадратов, а второй при их сумме. Соответственно эти варианты нужно будет дополнительно рассматривать для полного доказательства гипотезы Биля.