Теория игр. Парадокс в равновесии нэша для 2 участников.

[daniil_bj]

Здравствуйте, уважаемые участники форума!

Начнем с определения:
"Равновесие Нэша - это набор стратегий в игре для двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив свою стратегию, если другие участники своих стратегий не меняют."
Нэш доказал, что подобные равновесия (в чистых или смешанных стратегиях) должны существовать для всех конечных игр с любым числом игроков.

Имеем следующую конечную игру:

Есть 2 игрока, назовем их $sb$ (1) и $bb$ (2).
Для игры каждый из игроков имеет некоторое количество фишек $(stack)$, часть из которых он в обязательном порядке и указанном размере ставит в общий банк до начала игры (обязательные ставки), оставшиеся фишки остаются у игрока и могут быть использованы для ставки.
После выставления обязательных ставок каждый игрок получает некоторую комбинацию (руку), определяющую его силу в текущей игре.
Рука соперника не известна.

Ход игры:
Первым ходит $sb$, он имеет 2 возможных стратегии:
1. Сделать ставку, поставив все имеющиеся фишки в общий банк, и тогда ход переходит к $bb$.
2. Сбросить карты и тогда общий банк из первоначальных ставок переходит сопернику ($bb$) и игра заканчивается.

Если $sb$ увеличил ставку (стратегия 1), то у $bb$ так же есть выбор из 2 стратегий
1. Сделать ставку, поставив имеющиеся фишки в банк, после чего произойдет сравнение комбинаций и распределение банка в соответствие с их силой.
2. Сбросить руку и тогда sb получает банк, игра заканчивается.

(Оффтоп)

Сила одной руки относительно другой определяется некоторым значением, например рука “1” выигрывает у руки “2” в 4 случаев из 5.
Вероятности на победу для всех рук строго определены.
Для наглядности игра сильно упрощена. Игроков всего 2 и им доступны не все базовые 169 комбинаций, а всего 4: $AA, KK, AKs, AKo.$

В разбираемом примере обязательные ставки и стеки игроков составляют $blinds_s_b=50$, $blinds_b_b=100$ $stack_s_b_,_b_b=600$.

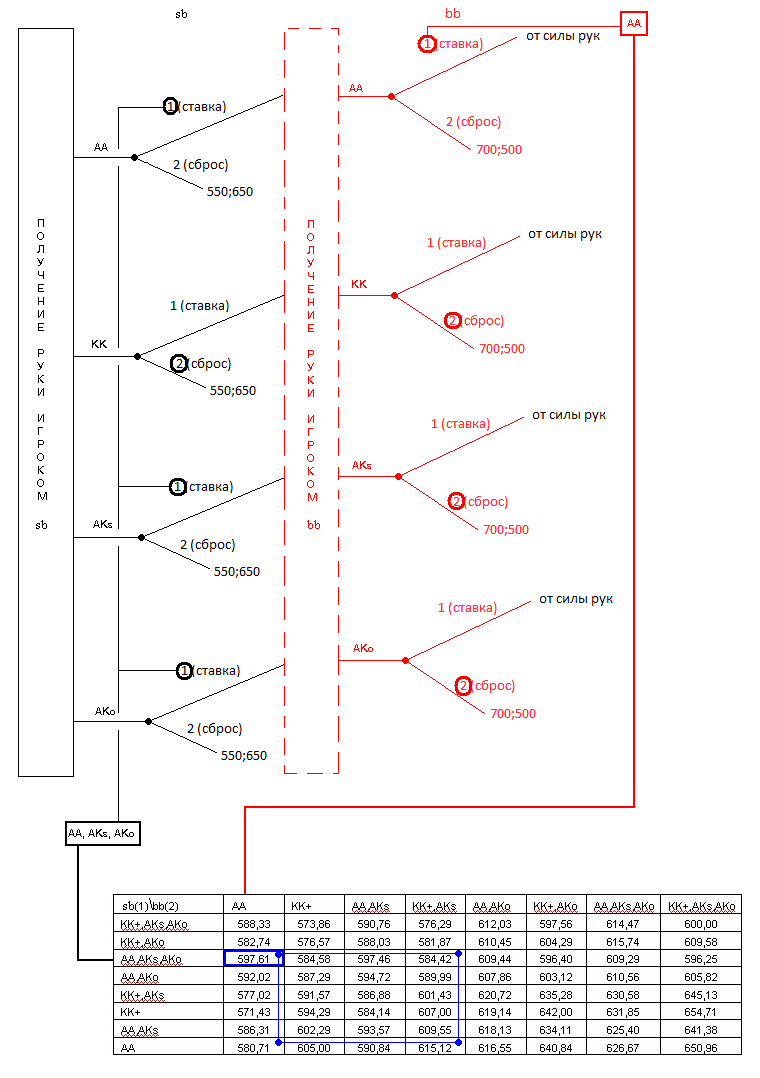
На рисунке показана игра в развернутой форме (вверху):
Вначале sb получает информацию о том, какая у него рука, $sb$ принимает решение, будет ли он ставить (стратегия 1) или сбрасывать (стратегия 2).
bb, если до него доходит ход, получает информацию о своей руке, принимает решение, будет ли он ставить (стратегия 1) или сбрасывать (стратегия 2).
Стратегия игроков описывается перечислением действий во всех возникающих ситуациях.
Для игрока $sb$, перечисляя стратегии, применяемые при соответствующей руке в следующем порядке: $AA, KK, AKs, AKo$ общая стратегия, изображенная на рисунке (в черных кружках) будет выглядит как
$S_s_b {1211}$, для большего удобства укажем только тех руки, при которых играется стратегия 1 (ставка) - $AA,AKs,AKo$
В матрице (внизу) перечислены все возможные чистые стратегии для обоих игроков, в ячейке на пересечении данных стратегий указан результат $P$ игрока $sb$.

(Оффтоп)

т.к. игра с нулевой суммой, то Pbb=(600+600)-Psb
АА присутствует во всех стратегиях для экономии места, поскольку набор действий со стратегией 1 (ставка) при руке АА строго доминирует идентичный набор с решением 2 (сброс) при руке АА.

Должно иметься минимум одно равновесие Нэша в чистых или смешанных стратегиях.

1. Попробуем найти равновесие в чистой стратегии.
Очевидно, что в матрице отсутствует равновесие по нэшу в чистых стратегиях, поскольку ни одна ячейка матрицы не является ячейкой с минимальным значением в строке (к этому стремится $bb$, увеличить свой выигрыш при выбранной стратегии $sb$) и одновременно с самым высоким значением в столбце (к этому стремится $mb$, увеличить свой выигрыш при выбранной стратегии $bb$).
Попытка выбора наиболее выгодной стратегии, при известной стратегии оппонента приводит нас к "закольцовыванию", помеченному в матрице прямоугольником с вершинами на пересечениях данных стратегий.

Один из игроков всегда может увеличить свой выигрыш при зафиксированной чистой стратегии оппонента, следовательно равновесия в чистых стратегиях в данной игре нет.

2. Предположим, что равновесие Нэша находится в смешанных стратегиях.
Решение в смешанных стратегиях подразумевает, что для некоторых рук действие 1 (ставка) будет выбрано с некоторой вероятностью (отличной от 0 и 1), например, при смешивании стратегий
${AA, AKs}$ 0,7
${AA AKs AKo}$ 0,3
смешанная стратегия будет иметь вид:
$AA 1, AKs 1, AKo 0,3$

Если отдельно рассмотреть ситуацию, когда игроком mb получена рука $AKo$ и сравнить решения 1 и 2, то одно из этих решений окажется более выгодным (при совпадении платежей при действиях 1 и 2 смешанная стратегия не имеет смысла и сводится к чистой).

Если при стратегии 1 (ставка) результат меньший, чем при решении 2, то не играя при руке $AKo$ стратегию 1 вовсе (соответственно применяя стратегию 2 в 100% случаев), игрок повышает свой выигрыш против (любой) фиксированной стратегии оппонента, что противоречит определению равновесия.
То же самое происходит, если при решении 1 получается больший платеж, чем при решении 2, то игрок может повысить свой выигрыш против стратегии оппонента, играя стратегию 1 (ставка) всегда (100% случаев, вместо 30% - как указано в примере).

Таким образом мы приходим к выводу, что равновесия Нэша в смешанной стратегии для данной задачи так же быть не может.

Однако, равновесие по Нэшу существовать должно, ибо игра конечная.
Можете указать на ошибку в рассуждениях?

[atlakatl]

Не понял рассуждений ТС. Но вот это откуда?

daniil_bj в сообщении #1177983 писал(а):

Если при стратегии 1 (ставка) результат меньший, чем при решении 2, то не играя при руке $AKo$ стратегию 1 вовсе (соответственно применяя стратегию 2 в 100% случаев), игрок повышает свой выигрыш против (любой) фиксированной стратегии оппонента

Рассмотрим простейшую игру.
Двое одновременно кладут в банк по одной или две монеты. Если сумма монет чётная, их забирает А, нечётная - В.
При "неигрании одним из игроков одной из стратегий" второй легко выигрывает у него.
А в смешанной стратегии равновесие Нэша вполне себе есть.
Попробуйте разобраться с этой задачей - найти смешанные стратегии для обоих - станет понятно, почему только смешанная стратегия и возможна.

[daniil_bj]

atlakatl

Ваша мысль понятна, в приведенной Вами задаче очевиден ответ: играть 0,5 стратегию 1 монета и 0,5 стратегию 2 монеты.
Поскольку при смешивании обе стратегии дают одинаковый результат вне зависимости от стратегии оппонента.

Отличие приведенной мной задачи в том, что
1. Каждый игрок кладет не 1 раз монеты, а 4.
2. Каждое из решений (1 или 2 монеты) влияет не на 1 банк, а на 4.


Если решение данной задачи и есть, то оно может быть только в чистых стратегиях (в матрице видно, что равновесия нет).
Приведенная задача интересна именно тем, что любая из сторон применяющая смешанную стратегию может увеличить свой выигрыш против фиксированной стратегии оппонента (не важно, чистой или смешанной), переходя в чистую.
А перейдя в чистые стратегии равновесия Нэша не находится.

[atlakatl]

daniil_bj
Вы ошиблись в моей задаче. Там для А одну монету нужно класть в $2/3$ случаях.
Функция выигрышей для А имеет вид:
$f(x, y)=xy+2(1-x)(1-y)-x(1-y)-2(1-x)y$
Здесь x и y вероятности выкладывания одной монеты каждым из игроков.
Попробуйте в своей задаче задаться конкретными значениями, посмотрите, что получится.
Но предварительно потренируйтесь на более лёгких примерах.

[daniil_bj]

Да-да, я невнимательно прочел, приняв задачу за совпадут или не совпадут орел/решка.
При перемножении 1/2 при сумме 2/3, поскольку нечет 1, чет 2 варианта.

У меня в задаче конкретные значения взяты.

[atlakatl]

daniil_bj
Всё-таки упростим Вашу задачу.
Первоначальный взнос 1 рубль для каждого.
Игрок S получает «руку», которая представляет собой равномерно распределённую случайную величину на интервале $(0; 1)$. S может положить 1 рубль или пасануть.
Игрок B смотрит свою «руку» – она такая же – и в свою очередь решает, положить свой рубль или пасануть.
Разберите эту задачу, может, всё встанет на свои места.

[daniil_bj]

atlakatl

Дело в том, что при более простых случаях как раз все сплошь и рядом в чистых стратегиях Нэш.
По сути, все сводится к предположению, что чистая стратегия всегда лучше смешанной.
Стратегия с некоторой частотой играть 1 и 2 может применяться только в том случае, если результат 1 и 2 совпадает.

PS
Я понимаю умом, что любая конечная игра содержит равновесие, пусть сложно находимое, но оно точно есть.
Вариантов стратегий конечное множество и любые подстройки войдут в цикл.
Но в этой задаче этого не происходит, не могу понять, почему.
4*4 - это сильное упрощение, оригинал 169*169 рук и не 2, а 10+ участников.

[atlakatl]

daniil_bj
А я не знаю, как аналитически решить мою - простую якобы - задачу.
Нужно найти 2 функции $f(x)$ и $g(y)$ (вероятности класть свой рубль), где x и y - "руки" каждого из игроков.
Расскажите, как Вы её решаете, будем двигаться дальше.

-- 18.12.2016, 14:52 --

daniil_bj в сообщении #1178006 писал(а):

все сводится к предположению, что чистая стратегия всегда лучше смешанной.

К чему сводить всё к абсурдному предположению?

[daniil_bj]

В вашей задаче есть странное правило. что рука 2го игрока "такая же".
Следовательно, 2й игрок, раз до него дошел ход будет играть стратегию 1.

Если не придираться к словам, то вы описали мою же задачу, только с цифр 50-100/600 перешли на 0-0/1
Обязательные ставки по 0, стек 1 рубль.

Задача решается через матрицу, если имеется решение в чистых стратегиях или через максиминное уравнение с 8 переменными (по 4 для каждого игрока) (могу быть не прав).
Его составляли в общем виде на бумаге, но в лоб к решению еще не перешли.

Вопрос остается - каким образом смешаная стратегия может быть эффективнее чистой, если рука, играемая стратегией 1 в интервале $(0;1)$ позволяет улучшить результат, сведя частоту использования стратегии 1 для этой руки строго к 0 или 1?

-- 18.12.2016, 14:52 --

К чему сводить всё к абсурдному предположению?[/quote]
Если вы читали пункт 2, то там объясняется, почему чистая стратегия дает больший выигрыш, чем смешанная.
Единственный случай, когда допускается смешивание, когда стратегия 1 и 2 руки, в которой различаются стратегии, дают идентичный результат.
Так что ничего абсурдного.

[atlakatl]

daniil_bj в сообщении #1178022 писал(а):

В вашей задаче есть странное правило. что рука 2го игрока "такая же".
Следовательно, 2й игрок, раз до него дошел ход будет играть стратегию 1.

У B выпало 0,001. И всё равно он будет класть свой рубль?

[daniil_bj]

А теперь не понимаю я.
Что такое 0,0001?

[atlakatl]

daniil_bj
У кого выпавшее ему число больше, тот и забирает банк. Второму игроку досталось число 0,001.

[daniil_bj]

Тогда все правила укажите.
Игрок 1, получая число что-то теряет, если не ставит?

[atlakatl]

daniil_bj
Я их написал ранее

atlakatl в сообщении #1178005 писал(а):

Первоначальный взнос 1 рубль для каждого.

-- 18.12.2016, 16:39 --

Кстати, будьте добры при написании своего комментария кликать по нику собеседника.
Он тогда в его профиле загорается красным цветом.

[DeBill]

daniil_bj

Вы неправильно понимаете слово "стратегия" применительно к этой игре.
Чистая стратегия первого- это когда товарищ , для каждой силы руки, сразу говорит, играет он или пасует.
Если возможных сил - сто, то чистых стратегий у первого - $2^{100}$...Ясно, что там есть стратегии, доминирующие одна другую. Так что , можно считать, что чистых стратегий - 101 (стратегия $k$ - это когда игрок пасует при силе ниже $k$, и делает ставку - в противном случае).
Аналогично, после чистки, у второго - тоже 101 чистая стратегия.
Вот теперь составляем матрицу стоодин на стоодин, и - вперед....

(Оффтоп)

Т.е., Ваша игра - это модель для покера.
Нда, предлагал я ее в качестве курсовой...И даже - с двумя кругами торговли... Для начала мы играли колодой из трех (а потом и из четырех!) карт, каждый получал по карте....А в последующей дипломной - ....