2) Допустим вдобавок, что в последовательности угловых миноров не встречается двух нулей подряд. Докажите, что в этом
случае отрицательный индекс инерции равен числу перемен знака в этой последовательности (или, точнее, в последовательности, получающейся из нее удалением нулей).
Займёмся вторым пунктом. Пусть в нашей последовательности миноров

нет двух нулей подряд. Нужно научиться бороться в этой последовательности с «дырами», то есть переходить к такому базису, чтобы нулевых миноров не стало.
Пункт 1. Возьмём первый нулевой минор

в последовательности

. Поменяем местами сначала последнюю и предпоследнюю строку, а затем последний и предпоследний столбец в матрице

, получим матрицу

(эта матрица является матрицей билинейной формы в базисе с поменянными векторами

, то есть

), при этом

. Далее возможно два случая:
1. Если

, перенумеруем (поменяем местами) векторы

и

. Получим новую последовательность миноров

, при этом

(при

), ибо при перенумерации векторов одновременно меняются строки и столбцы, а

.
2. Если

, перейдём к новому базису

. Покажем, что определитель

матрицы

, соответствующей угловому минору в новом базисе, не равен нулю.

Разобьём определитель по последней строке и обозначим получившиеся определители как
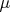
и


Теперь разобьём эти два определителя по последнему столбцу:


Так как

и

(в силу симметричности и того, что получившаяся матрица определителя
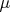
является транспонированной матрицей определителя

), можно заключить, что

В силу доказанного в предыдущем посте последняя строка

является линейной комбинацией первых

строк. Вычитая из последней строки

данную линейную комбинацию, мы занулим в последней строке первые

элементов, а последний будет
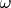
(в обозначениях предыдущего поста). Таким образом:

В силу того, что

, а значит,

, и

, можно заключить, что

.
Пункт 2. Итак в обоих случаях мы получили новую последовательность миноров

, в которой

. Покажем, что эти последовательности имеют одинаковое число перемен знака.
В первом случае 
(при

), а также

. Значит, каков бы ни был знак

, число перемен знака останется прежним.
Во втором случае 
(при

). Покажем, что при

и

знаки миноров останутся прежними, то есть

. По формуле перехода в новый базис при

имеем

, где

— матрица перехода, определитель которой равен

. Следовательно,

, то есть и в этом случае число перемен знака осталось прежним.
Пункт 3. Если в новой последовательности миноров

остались нули, возьмём первый нулевой минор и проделаем с ним данный алгоритм. Получим новую последовательность с тем же числом перемен знака, но уже без нулевого минора. Таким образом мы придём к последовательности без нулей.
Пункт 4. Новый базис, в котором нет нулевых миноров допускает ортогонализацию Грама — Шмидта, поэтому отрицательный индекс инерции равен числу перемен знака в новой последовательности, а значит равен числу перемен знака и в старой последовательности

.
Q.E.D.Обсуждение. Утверждение Якоби доказано, но Винберг предлагал модифицировать сам процесс ортогонализации. Видимо, решение проще? Хотя, как мне видится, концептуально и моё решение весьма простое (либо меняем базисные векторы местами, либо вместо первого берём их сумму, а вместо второго — разность). Думаю, на основе данного алгоритма можно модифицировать процесс ортогонализации.
Как можно интерпретировать результат данного метода? Что нового привносит базис

? Я, честно говоря, взял его наугад, но это почему-то сработало. Как можно интерпретировать переход к такому базису? И можно ли простым языком объяснить, почему это сработало?
(Оффтоп)
vpb, спасибо за пожелания. Вас тоже с прошедшим наступающим.