Доброго времени суток.
Пусть даны

различный чисел

из отрезка
![$[a,b],$ $[a,b],$](https://dxdy-02.korotkov.co.uk/f/9/9/1/991aa51d5284a7147f0cf3ee6ba9abfb82.png)
где

и еще

чисел

которые принимают значение либо 1, либо -1.
Обозначим

Возник следующий вопрос:
Правда ли, что независимо от распределения
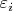
, существует такое число

что

?
Другими словами, правда ли, что как бы мы не расставили плюсы и минусы между числами

мы либо получим

либо не сможем приблизить значение

к нулю, ближе некоторой границы, зависящей только от

и

?
К примеру, если рассмотреть тривиальный случай, когда

то очевидно

Встречал ли кто то такую задачу или результаты, связанные с ней?
Спасибо.