Разложение степенных рядов на множители

[Ultramarine]

У меня тут свободное время появилось, поэтому я решил вас еще немного помучить вопросами.

¿ Правда ли что любой степенной ряд можно разложить на множители как:

$\sum\limits_{i=1}^{\infty}(a_i \cdot t^i)=a_0+a_1 \cdot t+a_2 \cdot t^2+\dots=$
$=a_0\prod\limits_{i=1}^{\infty}(1-\dfrac{t}{t_i})=a_0(1-\dfrac{t}{t_1})(1-\dfrac{t}{t_2})(1-\dfrac{t}{t_3})\dots$,

где $t_1, t_2, t_3, \dots$ — корни степенного ряда.

?

[Sonic86]

Есть тривиальный контрпример среди элементарных функций. Появляется в самом начале анализа целых функций.
Вы, кстати, избыточно предполагаете, что корней - бесконечное число.

[ИСН]

И что они вообще есть.

[Otta]

И что любой степенной ряд сходится в более чем одной точке. И вообще много чего.

[Ultramarine]

Otta в сообщении #1173338 писал(а):

И что любой степенной ряд сходится в более чем одной точке.

Согласен, необходимо добавить, что степенной ряд должен сходиться.

Sonic86 в сообщении #1173328 писал(а):

Есть тривиальный контрпример среди элементарных функций. Появляется в самом начале анализа целых функций.

Я знаю только разложение синуса/косинуса в бесконечное произведение... Что я упустил?

Sonic86 в сообщении #1173328 писал(а):

Вы, кстати, избыточно предполагаете, что корней - бесконечное число.

Уникальных корней может быть и конечное число. Например,

$(x+2)(x+1)=x^2+3x+2$ — два уникальных корня.
$\sqrt{x^2+3x+2}=\sqrt{(x+2)(x+1)}$ — тоже два уникальных корня, которые достались "по наследству" от многочлена выше, но $\sqrt{x^2+3x+2}$ — это бесконечный степенной ряд, чтобы его получить из этих уникальных корней, надо их тиражировать в бесконечном количестве. Разве не?

ИСН в сообщении #1173330 писал(а):

И что они вообще есть.

У степенных рядов ведь всегда есть как минимум один корень (пусть может быть и комплексный)?

[Sonic86]

Ultramarine в сообщении #1173348 писал(а):

Я знаю только разложение синуса/косинуса в бесконечное произведение... Что я упустил?

Просто переберите обычные элементарные функции, которые Вы знаете.

Ultramarine в сообщении #1173348 писал(а):

У степенных рядов ведь всегда есть как минимум один корень (пусть может быть и комплексный)?

не-а

[Ultramarine]

Sonic86 в сообщении #1173358 писал(а):

Ultramarine в сообщении #1173348 писал(а):

Я знаю только разложение синуса/косинуса в бесконечное произведение... Что я упустил?

Просто переберите обычные элементарные функции, которые Вы знаете.

Сложение/вычитание, умножение/деление, возведение в степень/извлечения корня. Хм?

Sonic86 в сообщении #1173358 писал(а):

Ultramarine в сообщении #1173348 писал(а):

У степенных рядов ведь всегда есть как минимум один корень (пусть может быть и комплексный)?

не-а

Даже если степенной ряд сходится?


А вообще вот как я рассуждал:

Многочлены являются "близкими родственниками" степенных рядов и допускают разложение на множители:

$\sum\limits_{i=0}^{n}(b_i \cdot t^i)=b_0+b_1 \cdot t + b_2 \cdot t^2 + \dots + b_n \cdot t^n=$
$=b_n(t-t_1)(t-t_2)(t-t_3)\dots(t-t_n)=b_n\prod\limits_{i=1}^{n}(t-t_i)$

Поэтому я подумал что степенной ряд тоже можно разложить на множители:

$\sum\limits_{i=0}^{\infty}(a_i \cdot t^i)=a_0+a_1 \cdot t+a_2 \cdot t^2+\dots=$
$=a_\infty(t-t_1)(t-t_2)(t-t_3)\dots=a_\infty\prod\limits_{i=1}^{\infty}(t-t_i)$

Если вынести все корни за скобки получим:

$a_\infty t_1 t_2 t_3 \dots (\dfrac{t}{t_1}-1)(\dfrac{t}{t_2}-1)(\dfrac{t}{t_3}-1)\dots$

Затем я воспользовался последней строчкой теоремы Виета для многочленов, которая гласит:

$t_1 t_2 t_3 \dots t_n = (-1)^n \dfrac{b_0}{b_n}$

... а значит для степенного ряда будет...

$t_1 t_2 t_3 \dots = (-1)^\infty \dfrac{a_0}{a_\infty}$

$a_\infty t_1 t_2 t_3 \dots (\dfrac{t}{t_1}-1)(\dfrac{t}{t_2}-1)(\dfrac{t}{t_3}-1)\dots=$
$=a_\infty (-1)^\infty \dfrac{a_0}{a_\infty} (\dfrac{t}{t_1}-1)(\dfrac{t}{t_2}-1)(\dfrac{t}{t_3}-1)\dots=$
$=a_0(-1)(\dfrac{t}{t_1}-1)(-1)(\dfrac{t}{t_2}-1)(-1)(\dfrac{t}{t_3}-1)\dots=$
$=a_0(1-\dfrac{t}{t_1})(1-\dfrac{t}{t_2})(1-\dfrac{t}{t_3})\dots=a_0\prod\limits_{i=1}^{\infty}(1-\dfrac{t}{t_i})$

[ИСН]

Логично выглядящие рассуждения за гранью формальной строгости могут принести полезный результат, а могут и бессмыслицу. С этой темой ситуация такая: всё вкусное нашёл Эйлер, а Вам досталось то, что осталось.

Ultramarine в сообщении #1173348 писал(а):

$\sqrt{x^2+3x+2}=\sqrt{(x+2)(x+1)}$ — тоже два уникальных корня, которые достались "по наследству" от многочлена выше, но $\sqrt{x^2+3x+2}$ — это бесконечный степенной ряд, чтобы его получить из этих уникальных корней, надо их тиражировать в бесконечном количестве. Разве не?

Куда и как Вы их собираетесь тиражировать? У этого выражения действительно два корня, унаследованных от многочлена; их два, их не будет больше.
И да, есть по крайней мере один ряд, сходящийся везде, но имеющий меньше корней, чем Вы думаете.

[B@R5uk]

Ultramarine в сообщении #1173365 писал(а):

Многочлены являются "близкими родственниками" степенных рядов

Вот этим родство на самом деле не родство, а просто совпадение фамилии. Предельный переход (который неизбежно имеется в степенном ряде) может творить чудеса, выводя явление на совершенно другой уровень. Например, множество рациональных чисел (которое счётное, то есть все его элементы можно пронумеровать от 1 до бесконечности) предельным переходом превращается в множество действительных чисел, которое уже не счётное. Чувствуете силу?

-- 01.12.2016, 19:12 --

Ultramarine в сообщении #1173365 писал(а):

Поэтому я подумал что степенной ряд тоже можно разложить на множители...

А вот возьмите и проведите численный эксперимент: ряд для каких-нибудь экспоненты, логарифма или корня оборвите на 1-ом, 2-ом, 3-ем, 4-ом, 5-ом, 6-ом члене и посмотрите какие кони будут иметь получившиеся полиномы. Будут ли вообще корни иметь что-то общее (я уж молчу про стремиться к чему-нибудь разумному) или же каждый раз будет получаться свой уникальный (в плане расположения корней) полином?

-- 01.12.2016, 19:31 --

Кстати, с экспонентой вообще забавная ситуация: в комплексной плоскости она нигде не обращается в нуль, что категорически противоречит вашему предположению о возможности разложения бесконечного ряда на множители.

[arseniiv]

Её таки назвали всуе.

[DeBill]

Ultramarine
Посмотрите в Вики: Теорема Вейерштрасса о целых функциях

[Ultramarine]

Sonic86 в сообщении #1173358 писал(а):

Просто переберите обычные элементарные функции, которые Вы знаете.

B@R5uk в сообщении #1173415 писал(а):

Кстати, с экспонентой вообще забавная ситуация: в комплексной плоскости она нигде не обращается в нуль, что категорически противоречит вашему предположению о возможности разложения бесконечного ряда на множители.

arseniiv в сообщении #1173470 писал(а):

Её таки назвали всуе.

А ну да...

В свое оправдание скажу, что я тоже вспомнил про экспоненту, когда вечером полистал учебники в поисках этой "загадочной" функции.

Действительно, экспоненту можно представить как

$e^x=\lim\limits_{n\to\infty}^{}\bigl( (1+\dfrac{x}{n})^n \bigr)=$

Если погрешить математической строгостью, то можно записать это как

$=(1+\dfrac{x}{\infty})(1+\dfrac{x}{\infty})(1+\dfrac{x}{\infty})\dots$

И тогда согласно вышеизложенному

Ultramarine в сообщении #1173322 писал(а):

¿ Правда ли что любой степенной ряд можно разложить на множители как:

$\sum\limits_{i=1}^{\infty}(a_i \cdot t^i)=a_0+a_1 \cdot t+a_2 \cdot t^2+\dots=$
$=a_0\prod\limits_{i=1}^{\infty}(1-\dfrac{t}{t_i})=a_0(1-\dfrac{t}{t_1})(1-\dfrac{t}{t_2})(1-\dfrac{t}{t_3})\dots$,

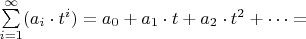
где $t_1, t_2, t_3, \dots$ — корни степенного ряда.

?

... получаем что $a_0=1$ и $x_1=x_2=x_3=\dots=-\infty$ (!), где $x_1, x_2, x_3, \dots$ — корни степенного ряда, полученного из $e^x$:

$e^x=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dots+\dfrac{x^n}{n!}+\dots$

Но $e^x$ не имеет корней в комплексной плоскости, так как

$e^{x+iy}=e^x(\cos(y)+i\sin(y))$

$\cos(y)+i\sin(y)\ne 0$, т.к. чтобы получить ноль, надо избавиться от $i$, а это можно сделать при $y=0$ или $y=\pi$, но при этих значениях $y$ значение $\cos(y)=\pm1$. Т.е. выражение никак не зануляется.

И $e^x>0$ при любом комплексном x... Хотя, если считать что $e^{-\infty}=0$, то озвученное в первом сообщении предположение работает (со скрежетом ) и в этом случае, но тут мы вступаем на зыбкие пески актуальной бесконечности.

[Aritaborian]

Ultramarine в сообщении #1174273 писал(а):

но тут мы вступаем на зыбкие пески актуальной бесконечности.

Можно считать, что не вступаем, если оперировать на сфере Римана ;-) А вообще актуальная бесконечность это чушь, бред и мистика, а никак не математика.

[ewert]

Ultramarine в сообщении #1174273 писал(а):

Хотя, если считать что $e^{-\infty}=0$,

Нельзя так считать -- в комплексной плоскости нет минус бесконечности. есть только просто бесконечность; точка вполне почтенная, но у экспоненты в ней -- отнюдь не ноль.

Ultramarine в сообщении #1174273 писал(а):

И $e^x>0$ при любом комплексном x..

Это сильно вряд ли.

[Ultramarine]

Aritaborian в сообщении #1174275 писал(а):

Ultramarine в сообщении #1174273 писал(а):

но тут мы вступаем на зыбкие пески актуальной бесконечности.

А вообще актуальная бесконечность это чушь, бред и мистика, а никак не математика.

Согласен, актуальная бесконечность дает меньше, чем забирает.

Но просто, мне показалось, что в математике не все так думают. Вон в интернете гуляют книжки по нестандартному анализу, в которых на бесконечно малые и бесконечно большие числа смотрят как на "обычные" числа и оперируют с ними наравне с "обычными" числами.

https://ru.wikipedia.org/wiki/Нестандартный_анализ

ИСН в сообщении #1173385 писал(а):

Ultramarine в сообщении #1173348 писал(а):

$\sqrt{x^2+3x+2}=\sqrt{(x+2)(x+1)}$ — тоже два уникальных корня, которые достались "по наследству" от многочлена выше, но $\sqrt{x^2+3x+2}$ — это бесконечный степенной ряд, чтобы его получить из этих уникальных корней, надо их тиражировать в бесконечном количестве. Разве не?

Куда и как Вы их собираетесь тиражировать? У этого выражения действительно два корня, унаследованных от многочлена; их два, их не будет больше.

Ну я рассуждал как-то так. Вот есть график параболы. Пусть он к тому же лежит полностью выше оси Ox. Если из параболы извлечь квадратный корень, то мы получим новый график, который будет лежать между осью Ox и графиком параболы. Действительно, при тех $x$, где значение параболы будет равно 4, 9, 16, ... , значения корня квадратного из параболы будут 2, 3, 4, ... (отрицательные корни -2, -3, -4, ... упустим ).

А какой функцией будет описываться наш новый график квадратного корня из параболы? Наверняка степенным рядом. Но если как я предполагал верно что

Ultramarine в сообщении #1173322 писал(а):

¿ Правда ли что любой степенной ряд можно разложить на множители как:

$\sum\limits_{i=1}^{\infty}(a_i \cdot t^i)=a_0+a_1 \cdot t+a_2 \cdot t^2+\dots=$
$=a_0\prod\limits_{i=1}^{\infty}(1-\dfrac{t}{t_i})=a_0(1-\dfrac{t}{t_1})(1-\dfrac{t}{t_2})(1-\dfrac{t}{t_3})\dots$,

где $t_1, t_2, t_3, \dots$ — корни степенного ряда.

?

... то чтобы получить $x$ в "бесконечной степени" как в степенном ряде, то корни параболы придется "тиражировать": бесконечно перемножать друг с дружкой.

Т.е. я подумал что, например,

$\sqrt{x^2+3x+2}=\sqrt{(x+2)(x+1)}=\prod\limits_{i=1}^{\infty}\biggl( \Bigl( 1+\dfrac{x}{2} \Bigr) \Bigl( 1+\dfrac{x}{1} \Bigr) \biggr)$