Зависимость координат материальной точки/помогите решить

[Veltared]

Зависимость координат материальной точки по двум взаимноперпендикулярным направлениям описывается уравнениями:
$x(t)={10\sin2t}$
$y(t)={5\sin(2t+\pi/2)}$
Вычислите:
1. Зависимость скорости и ускорения от времени.
2. Скорости и ускорения в момент времени $t=0.5$ с.
3. Максимальную скорость точки.
4. Уравнение траектории движения точки.
5.Постройте график зависимости $y=f(x)$ и определите координаты точек траектории в которой скорость точки наибольшая и наименьшая изобразить их на графике.
Пожалуйста объясните что необходимо сделать,какие формулы нужно использовать и каким график будет выглядеть в конечном счете.В физике я полный 0,поэтому чем больше вы распишите тем лучше я пойму.

Мой прогресс решения на данный момент.

Формулы:
${sin2t}={x/10}$
${cos2t}={x/5}$
${sin^2a}+{cos^2a}={1}$ => ${sin^2t}+{cos^2t}={1}$ =>${(x/10)^2}+{(y/5)^2} = {1}$ => ${y/5}={1}-{(x/10)^2}$


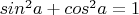
Уравнение параболы.

${(x/10)^2}+{(y/5)^2} = {1}$

Уравнение траектории через y.

${y=5-x^2/20}$
Области определения.
$x=0$ $y=5$.
$-10<={x}<=10$
$0<={y}<=50$
Положение точки в момент 0,5 с.
$x={10\sin(2t)}=10 см$
$y={5\cos(2t)}=5 см$
Компонент скорости.
$v(x)=20\cos(2t)$
$v(y)=-10\sin(2t)$
Определение модуля скорости.
t = 0
$v(x)=20\cos(2(0))=20$
$v(y)=-10\(sin2(0))=-10$
t = 1
$v(x)=20\cos(2(1))=?$
$v(y)=-10\(sin2(1))=?$
t = 1/2
$v(x)=20\cos(2(1/2))=0$
$v(y)=-10\(sin2(0))=0$
Комментарии:Возникла проблема с просчетом модуля скорости и ускорения.Без помощи дальше пока не могу продвинуться.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неинформативный заголовок;
- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.