Задачу придумал себе я. Препод тут не причём :)
Прежде всего: вот тут вы очень молодец! Нечего сидеть на месте и довольствоваться тем, что скармливают!
Но увы, есть такие разделы математики (чёрт, да их большинство!), где задачи примерно распадаются на две группы:
- те, которые можно решить, сравнительно простые, и может быть, даже кому-то скучные;
- те, которые записываются хотя бы чуть-чуть сложнее, но решить их безумно сложно или невозможно вовсе.
Математика - это как ходить по болоту. Чуть-чуть оступишься, и провалишься. (Некоторое спасение можно найти в примерных вычислениях, например, в численном интегрировании.)
И можете помочь с поиском этого интеграла?
А вы смелый? Это материал первого-второго года вуза, "математический анализ функций нескольких переменных" (плюс немного "аналитической геометрии").
Суть в том, что искомый интеграл - это
интеграл по поверхности. Это вам могли рассказывать на физике: вы разбиваете на малые элементы

не числовую ось

а некоторую поверхность
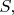
так что получаются элементы

(численно каждому элементу сопоставляется его площадь, отсюда и обозначения). Такой интеграл записывается в виде

Сама функция

может быть при этом задана во всём объёме -

- но это не обязательно. Главное, чтобы она оказалась задана во всех точках, где проходит поверхность - поверхность интегрирования. Это общая идея интеграла по поверхности. А вам нужна более простая: вам нужно найти просто площадь поверхности. То есть, вы можете положить

и не задумываться о ней! :-) Вас интересует

Когда мы разбили поверхность на малые элементы, мы облегчили себе работу. Мы теперь имеем дело не с искривлённой поверхностью, а с кусочком плоскости. Поэтому, мы можем применять простые формулы.
Например, можно спроецировать (умные дядьки пусть как хотят, а я привык проецировать) этот кусочек плоскости на какую-нибудь из координатных плоскостей, например, на  Тогда мы можем заметить, что площади соотносятся так:
Тогда мы можем заметить, что площади соотносятся так:  где
где  - угол между нашим кусочком плоскости, и координатной плоскостью
- угол между нашим кусочком плоскости, и координатной плоскостью  А кусочек плоскости
А кусочек плоскости  можно принять прямоугольным, и тогда написать
можно принять прямоугольным, и тогда написать  (от выбора формы кусочка интеграл не должен зависеть). И таким образом, мы имеем двойной интеграл, который можем взять как повторный - интеграл от интеграла:
(от выбора формы кусочка интеграл не должен зависеть). И таким образом, мы имеем двойной интеграл, который можем взять как повторный - интеграл от интеграла:
 Ну или в другом удобном для нас порядке (не обязательно даже брать этот интеграл в декартовой системе координат по плоскости
Ну или в другом удобном для нас порядке (не обязательно даже брать этот интеграл в декартовой системе координат по плоскости  ). Совершенно аналогично можно взять проекцию на плоскости
). Совершенно аналогично можно взять проекцию на плоскости 
Нераскрыт только вопрос, как вычислить  Например, если поверхность задана как функция "рельефа местности"
Например, если поверхность задана как функция "рельефа местности"  то
то  будет прямоугольником, а
будет прямоугольником, а  - "поднятым" над ним параллелограммом. Стороны этого параллелограмма образуют с плоскостью
- "поднятым" над ним параллелограммом. Стороны этого параллелограмма образуют с плоскостью  углы, которые вычисляются через частные производные:
углы, которые вычисляются через частные производные:  - которые берутся от
- которые берутся от  по одной переменной при условии, что вторая переменная зафиксирована, "неподвижна". Как и для обычной производной, величина производной равна тангенсу соответствующего угла. Дальше используется ловкая замена: вместо угла между плоскостями, мы рассматриваем угол между нормалями (перпендикулярными к этим плоскостям прямыми), эти два угла равны между собой. А угол между нормалями можно вычислить через скалярное произведение двух векторов:
по одной переменной при условии, что вторая переменная зафиксирована, "неподвижна". Как и для обычной производной, величина производной равна тангенсу соответствующего угла. Дальше используется ловкая замена: вместо угла между плоскостями, мы рассматриваем угол между нормалями (перпендикулярными к этим плоскостям прямыми), эти два угла равны между собой. А угол между нормалями можно вычислить через скалярное произведение двух векторов:  и
и  (Вектор
(Вектор  нормален к плоскости
нормален к плоскости  потому что он нормален к двум пересекающимся прямым, лежащим в этой плоскости.) Таким образом,
потому что он нормален к двум пересекающимся прямым, лежащим в этой плоскости.) Таким образом,  и окончательно, после вычисления в координатах,
и окончательно, после вычисления в координатах,  Как видите, всё в конечном счёте можно вычислить средствами матанализа, геометрии и векторного исчисления.
Как видите, всё в конечном счёте можно вычислить средствами матанализа, геометрии и векторного исчисления.
Такой "прямолинейный" способ позволяет справиться с ситуациями общего вида, но в вашем случае я бы его не советовал. Лучше использовать хорошую форму рассматриваемой поверхности, и разбить её на кусочки удобного вида, которые потом можно будет легко собрать вместе. Один из способов вам предлагает (намёками)
Red_Herring.