2. (Пора различать верхние и нижние индексы.) Действительно, в каждой точке базис

будет дуальным к

, где

. В частности,

.
Далее, скалярное произведение двух базисных векторов равно соответствующей компоненте метрического тензора:

,
откуда

(без суммирования).
В полярных (и цилиндрических) координатах

, т.е. длина базисного вектора
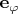
в данной точке равна

. (См. Г.Корн, Т.Корн, Справочник по математике, стр.186, таблица 6.5-1, строка «Квадрат элемента длины».) Иными словами,
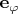
— это базисный вектор, но не орт.
Такова ситуация в дифференциальной геометрии. Но в приложениях (инженерных и большей части физических, за исключением ОТО и некоторых других разделов физики) используется другой стандарт — ортонормированный базис всюду, где только возможно. «Физические», т.е. ортонормированные базисные векторы, обозначим через

, чтобы не смешивать с

. В ортогональных системах координат они получаются из

так:

Вы, собственно, вычисляли

Преимущества дифференциально-геометрического определения: более простая и естественная теория; простой закон преобразования компонент при замене базиса.
Преимущества физического определения: более простая интерпретация компонент с точки зрения практики. Но, как следствие, «физический» базис

оказывается некоординатным, соответствующие векторные поля не коммутируют и т.д. Да и применим подобный подход лишь там, где используются ортогональные системы координат.
, спасибо за обстоятельный ответ! Этот пример я нашел изучая книгу Арнольда, и про другую нормировку базиса он тактично умолчал, а у меня заворот мозга случился
 -- 07.06.2016, 16:54 --
-- 07.06.2016, 16:54 --Неформально говоря, отображение

из

в

позволяет протянуть
вперёд (pushforward) векторные поля, и
назад (pullback) дифференциальные формы (любой степени, начиная с 0-форм — функций на

). Отображения, обратные указанным, могут и не существовать. Полезное упражнение — понять, почему именно так; почему, например, заданное

естественно переносит скалярные функции с

на

, а не наоборот.
Да, я накосячил со звездочкой, а исправить форум не дает :(
Но ведь дифференциал-это функция, кушающая вектор и выдающая опять функцию, а не касательный вектор.
Только в случае, если размерность

равна единице. В случае же отображений

, где

, у Вас появится

вещественных функций на

, которые интерпретируются как компоненты «выходного» векторного поля.
Действительно, мы получаем

размерное пространство функций, но ведь должны были прыгнуть в

мерное пространство дифференциальных операторов? Пространство дифф операторов и дифференциалов дуальны друг другу, и преобразуются по разному.
Если читаете по-английски, то: M.Spivak, A Comprehensive Introduction to Differential Geometry, p. 109-112. Хорошее обсуждение взаимосвязи между дифференциалами функции в анализе, отображения в дифгеме, дифференциальной формы.
Спасибо за книгу, сижу изучаю. К сожалению, проблема не в английском, а в том что почти все книги по дифф геометрии немного ортогональны друг другу, и начав чтение нового автора эквивалентно изучению предмета с чистого листа :)