Всем добрый день. Есть задача из Волковыского,не поддающаяся решению. Укажу её номер,по современным задачникам.
Номер 2.44. Доказать,что при отображении круга на круг линейное преобразование однозначно определяется заданием образов одной внутренней и одной граничной точек.
Моя попытка решения:
Не нашёл хорошей литературы по данному вопросу,но нечто подобное заметил у Привалова,"Введение в ТФКП"(страница 116). Там говорится,что если мы имеем окружность радиуса

, две точки

и

,симметричные относительно данной окружности,то с помощью произвольного линейного преобразования "пара взаимно симметричных точек перейдёт в пару точек,взаимно симметричных относительно отображенной окружности". При доказательстве берётся за основу тот факт,что через точку

и произвольную точку

(вот где задействовано наше условие из номера!) основной окружности,можно провести окружность,ортогональную к основной,и при том только одну(это окружность превращается в прямую
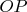
, если точка

лежит на данной прямой),таким образом задействованы и наша граничная точка

,и внутренняя точка

. У меня возник вопрос относительно того,справедливо ли данное рассуждение,и если оно верно,то почему данное преобразование определяется однозначно? (В силу единственности ортогональной окружности?)
Заранее спасибо за прочтение и размышления!
|
i |
Оформляйте даже единичные символы-обозначения. |