
Пусть
 -
- минимальное поле разложения многочлена

над полем
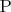
.
Докажите, что если

, то
![$\mathrm{[P':P]\le {m!}}$ $\mathrm{[P':P]\le {m!}}$](https://dxdy-02.korotkov.co.uk/f/9/9/f/99f50206125f6eb1644a4b8bf056697a82.png)
.
с этой частью задачи я разобрался с помощью теоремы о башне полей, но есть ещё 2 пункт
Докажите, что если
![$\mathrm{[P':P]=m!}$ $\mathrm{[P':P]=m!}$](https://dxdy-02.korotkov.co.uk/f/5/8/e/58e1ffe940859f12254d150e0fb86d9f82.png)
, то многочлен

неприводим над
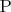
.
На что мне ссылаться при доказательстве? Хотелось бы внести ясность в этом вопросе.