Выражение 0^0

[Brukvalub]

Профессор Снэйп писал(а):

Надо сказать, что разного рода "неопределённости" в матане происходят исключительно из-за некорректного использования обозначений.

[bot]

А как рассматривать предел

Профессор Снэйп писал(а):

исходя из их теоретико-множественных определений

?
Вот такой, к примеру: $\lim\limits_{x\to 0^+} x^{\frac{1}{\ln x}}$

[Профессор Снэйп]

Brukvalub писал(а):

Профессор Снэйп писал(а):

Надо сказать, что разного рода "неопределённости" в матане происходят исключительно из-за некорректного использования обозначений.

А чем Вы удивлены?

Вот есть, допустим, теорема: если последовательности $\{ x_n \}_{n \in \mathbb{N}}$ и $\{ y_n \}_{n \in \mathbb{N}}$ сходятся к действительным числам $a$ и $b \neq 0$ соответственно, то последовательность $\{ x_n/y_n \}_{n \in \mathbb{N}}$ также сходится и её предел равен $a/b$. В теореме ничего не говорится о сходимости этой последовательности в случае, когда $b=0$. 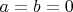Однако иногда (но не всегда) последовательность $\{ x_n/y_n \}_{n \in \mathbb{N}}$ при $a=b=0$ всё же сходится и тогда её предел ни с того ни с сего начинают трактовать как "одно из возможных значений неопределённого выражения $0/0$".

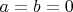
В случае, когда $b \neq 0$, выражение $a/b$, фигурирующее в теореме, имеет вполне чёткий, определённый смысл: это результат операции деления на ненулевой элемент в поле действительных чисел. При $a=b=0$ это теряет смысл и начинаются какие-то нелепые фантазии, которым может быть только одно оправдание: при надлежащей осторожности в обращении они экономят время, позволяя путём некорректных, но коротких выкладок приходить к правильному результату. Игры со значками --- это хорошо, играйте сколько влезет, но не надо пытаться придавать получающимся в ходе таких игр выражениям какой-то содержательный смысл, особенно "действуя по аналогии". Не делится ноль на ноль в $\mathbb{R}$ и всё тут, ибо операция взятия обратного элемента в поле по определению частичная. Попытки поделить, используя значения пределов частных --- они от лукавого.

То же самое с возведением в степень. Операция $x^y$ не определена на $\mathbb{R}$ при $x=y=0$ и говорить о значении выражения $0^0$ как о результате этой операции бессмысленно.

А между тем в другой области математики, более фундаментальной чем матан --- математической логике, есть 3 определения операции возведения в степень: одно для множеств, другое для ординалов, третье для кардиналов. Согласно всем трём определениям $0^0=1$. Так что ответ на исходный вопрос более чем очевиден.

Добавлено спустя 2 минуты 43 секунды:

bot писал(а):

А как рассматривать предел

Профессор Снэйп писал(а):

исходя из их теоретико-множественных определений

?
Вот такой, к примеру: $\lim\limits_{x\to 0^+} x^{\frac{1}{\ln x}}$

Вы хотите, чтобы я Вам в ZFC доказал, что значение этого предела равно $e$ или как?

[bot]

Да нет, не надо - просто предыдущее можно было понять совершенно в противоположном смысле.

Профессор Снэйп писал(а):

... тогда её предел ни с того ни с сего начинают трактовать как "одно из возможных значений неопределённого выражения 0/0"

Ну, здесь не очень много способных на такую трактовку.

Добавлено спустя 6 минут 23 секунды:

Однако даже уничижители нуля попадаются:
http://dxdy.ru/viewtopic.php?t=8116

[Brukvalub]

Профессор Снэйп писал(а):

А между тем в другой области математики, более фундаментальной чем матан --- математической логике....

Самая фундаментальная наука - мыловарение, без нее нас всех съедят блохи...

[Yarkin]

shwedka писал(а):

Нет, не так. В математике слова 'существует', 'не существует' имеют всегда вполне конкретный смысл, возникающий в результате определения.

Согласен. Но я, по моему, не нарушаю этот принцип. Свои выводы я сделал на основании определения тригонометрической формы к. ч.

[STilda]

Mathematica выдала Indeterminate. Это не арифметическая формула. Скорее это объект задающийся через его свойства. $0^0 : (0^0)^n=0^0 \&& ...$

[shwedka]

Yarkin

Цитата:

Свои выводы я сделал на основании определения тригонометрической формы к. ч.

Тригонометрическая форма нуля не определена.
Профессор Снэйп

Цитата:

Однако иногда (но не всегда) последовательность $\{ x_n/y_n \}_{n \in \mathbb{N}}$ при $a=b=0$ всё же сходится и тогда её предел ни с того ни с сего начинают трактовать как "одно из возможных значений неопределённого выражения $0/0$".

Не так. Студентов учат: неопределенность типа $0/0$. Педагогический прием, не имеющий отношения к реальному делению. Непределенное выражение не может иметь значения.

Цитата:

Согласно всем трём определениям $0^0=1$

Ну, давайте, продемонстрируйте мне отображение из пустого множества в пустое множество

[Профессор Снэйп]

Вот здесь написано, что $0^0=1$.

http://www.research.att.com/~njas/sequences/A000007

shwedka писал(а):

Ну, давайте, продемонстрируйте мне отображение из пустого множества в пустое множество

Я уже демонстрировал Могу подробнее разъяснить.

Определение. Функцией из множества $A$ в множество $B$ называется подмножество $f \subseteq A \times B$, такое что для любого $a \in A$ существует единственное $b \in B$, для которого $\langle a,b \rangle \in f$.

В случае $A=B=\varnothing$ множество $f = \varnothing$ удовлетворяет этому определению.

P. S. Вы уж мне поверьте, я уже не один год в НГУ этому студентов учу Если не верите --- найдите какую-нибудь хорошию книжку по теории множеств (основаниям математики, математической логике), там будет то же самое написано.

[Brukvalub]

Профессор Снэйп писал(а):

В случае $A=B=\varnothing$ множество $f = \varnothing$ удовлетворяет этому определению.

Вот и начало сказываться величие математической логики.

[shwedka]

Профессор Снэйп

Цитата:

существует единственное $b \in B$

Ну, и где это b ?? и докажите единственность.

[shust]

shwedka писал(а):

shust

Цитата:

неопределенность________ [ 31 ] [28.18%]

Путаница здесь. Вы спрашиваете о 'неопределенности' - это педагогический термин, относящийся к теории пределов.

В Швеции все такие рассеянные, как уважаемая "shwedka"?
В том посте я только цитирую результаты аналогичного опроса, проведенного по адресу, указанному несколько выше и не по моей инициативе. У меня там даже кавычки есть.

По поводу пункта "неопределенность" - это наверно жаргон у них там такой. Я же говорил, что они люди простые и, говорят, даже гуманитарии.

[Профессор Снэйп]

Не верють...

Логика математических утверждений иногда расходится с логикой повседневной жизни. Всё дело просто в том, что математики привыкли мыслить точно.

Пусть $\Phi(x)$ --- произвольное утверждение про некий объект $x$. Это может быть и утверждение о том, что $x$ --- простое число, и утверждение о том, что $x$ есть Римский Папа, и любое другое утверждение.

В чём бы не заключалось утверждение $\Phi$, утверждение $(\forall x \in \varnothing) \Phi(x)$ будет истинно всегда. Убедится в этом можно одним из двух способов. Во-первых, его можно переписать в эквивалентной форме $\forall x(x \in \emptyset \rightarrow \Phi(x))$ и заметить, что при любом $x$ в скобках стоит импликация с ложной посылкой, то есть истинное утверждение. Во-вторых, если предположить, что утверждение $(\forall x \in \varnothing) \Phi(x)$ ложно, то истинным должно быть его отрицание. Отрицание же эквивалентно утверждению $(\exists x \in \varnothing) \neg\Phi(x)$, ложность которого не подлежит сомнению (ну как вы найдёте элемент из пустого множества со свойством $\neg\Phi$, если в пустом множестве вообще нет элементов).

Теперь: берём $\Phi(a) = (\exists ! b \in \varnothing)(\langle a,b \rangle \in f)$. Естественно, $\Phi(a)$ будет ложным для любого $a$. Однако утверждение $(\forall a \in \varnothing)\Phi(a)$ --- истинно!!! И, значит, любое множество $f$ удовлетворяет второму условию из определения функции из $A$ в $B$ в случае, когда $A=B=\varnothing$.

Первое же условие заключается в том, что $f$ должно быть подмножеством $A \times B$. Ему удовлетворяет только пустое множество. Таким образом, пустое множество является единственным элементом множества функций из $\varnothing$ в $\varnothing$.

[Brukvalub]

Профессор Снэйп писал(а):

Логика математических утверждений иногда расходится с логикой повседневной жизни. Всё дело просто в том, что математики привыкли мыслить точно.

Нам, операторам машинного доения (читай - доярам) такой глубокий смысл без надобности. Ну зачем мне, положим, пустое множество коров (это что, получается - их всех на фарш отправили?). Такое стадо нам не нужно - кого же я тогда доить стану? А мне без дойки никак нельзя - мастерство зараз упадёт. Вот и получается - все правда, что я давно подозревал: эти математические логики дурят простого мужика, ох дурят... Фокусничают, понимаешь, с пустыми множествами и формализмом своим, будь он трижды неладен, смысл у бессмысленных выражений выискивают. Неужто это им и вправду душу греет?

[Профессор Снэйп]

Brukvalub писал(а):

Ну зачем мне, положим, пустое множество коров (это что, получается - их всех на фарш отправили?). Такое стадо нам не нужно - кого же я тогда доить стану?

Зато если множество коров в стаде пустое, то каждая корова из вашего стада --- рекордсмен области и даже республики по удоям! Причем любая корова также является и быком, рожает по 80 телят в месяц и имеет большие ветвистые рога, как у оленя. А во лбу у неё пулемёт, а глаза такие добрые-добрые...

Красная Бурда писал(а):

Уж как я мою коровушку люблю,
Топором рога бурёнке отрублю,
Хвост отрежу скоростной бензопилой,
Чтоб повысило животное удой.

Уж как я мою коровушку люблю,
Керосина в отрубя ей подолью,
Чтоб резва была бурёнушка моя,
Чтоб ревела реактивная струя.