Помогите пожалуйста решить такую задачу или хотя бы подскажите алгоритм решения.
3. В поле

, где

– корень многочлена

, найти элемент, обратный к

Предложили так находить:с помощью алгоритма евклида доказать,что нод этих многочленов равен 1.А потом получит разложение:

,потом вместо

в первом многочлене ставим

и это произведение обнуляется и таким образом получим
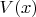
, который и будет ответом.
Но проблема втом,что у меня не получается нод этих многочленов равный 1.Или я что-то делаю не так или он не равен 1.