Пусть ненулевые, взаимно-простые целые числа

,

и

удовлетворяют уравнению Ферма:

,
где

- нечётное простое число.
Тогда

, где

.
Пусть

не делится на

.
Мы знаем, что
![$x^2-y z \sqrt[n]{4}$ $x^2-y z \sqrt[n]{4}$](https://dxdy-04.korotkov.co.uk/f/3/a/5/3a5d695aa3f95eb012eaca43f264200882.png)
является квадратом целого алгебраического числа поля
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
, при условии однозначности разложения на простые множители в этом поле.
В этой теме мы пытаемся получить новые результаты, не предполагая этой однозначности.
О том, что это возможно говорит, например, теорема Фуртвенглера для поля
![$\mathbb{Q}[i_n]$ $\mathbb{Q}[i_n]$](https://dxdy-03.korotkov.co.uk/f/e/9/8/e98a5e4e92018717c059cd9dc9d885d682.png)
.
В этой теореме играет роль делитель единицы

(комплексный корень

-ой степени из

).
В поле
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
, мы могли бы использовать делитель единицы
![$\sqrt[n]{2}-1$ $\sqrt[n]{2}-1$](https://dxdy-04.korotkov.co.uk/f/b/9/5/b954036352b44c1821d4f81f2c6a5f1d82.png)
.
Некоторые результаты я получил в теме "Новое доказательство ВТФ для n=3".
Упомянутая тема развивалась в немного другом направлении (мы доказывали в ней, что
![$x^2-y z \sqrt[3]{4}$ $x^2-y z \sqrt[3]{4}$](https://dxdy-02.korotkov.co.uk/f/9/f/7/9f7818efe8a4e439f7d60042c4b9ac4a82.png)
является суммой квадратов).
Но несколько результатов посвящены вопросу о том, по модулю каких простых чисел

, число
![$x^2-y z \sqrt[n]{4}$ $x^2-y z \sqrt[n]{4}$](https://dxdy-04.korotkov.co.uk/f/3/a/5/3a5d695aa3f95eb012eaca43f264200882.png)
сравнимо с квадратом.
В частности, если
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует по модулю

, то число
![$x^2-y z \sqrt[n]{4}$ $x^2-y z \sqrt[n]{4}$](https://dxdy-04.korotkov.co.uk/f/3/a/5/3a5d695aa3f95eb012eaca43f264200882.png)
сравнимо с квадратом по модулю

.
Заметим, что
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует по модулю

только если

.
Обозначим поле
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
через

, а кольцо целых алгебраических чисел этого поля через

.
Если
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует по модулю

, то

является простым идеалом кольца

.
Покажем это в оффтопике.
(Оффтоп)
Покажем, что если
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует по модулю

, то

является простым идеалом кольца

.
Предположим идеал

не является простым.
Тогда он разлагается в произведение

простых идеалов.
Пусть

- какой-либо из этих простых идеалов.
Тогда норма идеала

равна

, следовательно

является полной системой вычетов по модулю идеала

.
Значит число
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
сравнимо с элементом

по модулю идеала

.
Следовательно число

сравнимо с

-ой степенью целого числа по модулю идеала

, следовательно и по модулю

.
Значит
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
существует по модулю

.
Что и требовалось.
Теперь в другом оффтопике покажем, что если
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует по модулю

, то число
![$x^2-y z \sqrt[n]{4}$ $x^2-y z \sqrt[n]{4}$](https://dxdy-04.korotkov.co.uk/f/3/a/5/3a5d695aa3f95eb012eaca43f264200882.png)
сравнимо с квадратом по модулю

.
(Оффтоп)
Пусть
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует по модулю

.
Тогда идеал

является постым.
Следовательно
![$(x^2-y z \sqrt[n]{4})^{(p^n-1)/2}$ $(x^2-y z \sqrt[n]{4})^{(p^n-1)/2}$](https://dxdy-04.korotkov.co.uk/f/7/d/c/7dc53ac453e711061d9585b23ff48cff82.png)
сравнимо либо с

, либо с
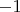
по модулю

.
Подставим в эти сравнения вместо числа
![$\sqrt[n]{4}$ $\sqrt[n]{4}$](https://dxdy-03.korotkov.co.uk/f/2/4/9/249b088fd9588ff7ad83532aba75926c82.png)
сопряжённые с ним числа и перемножим полученные таким образом сравнения.
Поскольку

является квадратом по модулю

, то

.
Значит
![$(x^2-y z \sqrt[n]{4})^{(p^n-1)/2} \equiv 1 \mod p$ $(x^2-y z \sqrt[n]{4})^{(p^n-1)/2} \equiv 1 \mod p$](https://dxdy-03.korotkov.co.uk/f/2/8/7/287050748d20734319f74feb3aeebd0282.png)
.
Следовательно число
![$x^2-y z \sqrt[n]{4}$ $x^2-y z \sqrt[n]{4}$](https://dxdy-04.korotkov.co.uk/f/3/a/5/3a5d695aa3f95eb012eaca43f264200882.png)
сравнимо с квадратом по модулю

.
Заметим, что среди простых чисел, сравнимых с

по модулю

, числа, по модулю которых
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
не существует, встречаются гораздо чаще чисел по модулю которых
![$\sqrt[n]{2}$ $\sqrt[n]{2}$](https://dxdy-02.korotkov.co.uk/f/9/2/5/9257194dc6a0fbd0b6f9f0847ce7095982.png)
существует (согласно компьютерной проверке).
Наша следующая задача доказать новый результат.
Пусть

- такое простое число, что квадратичный символ
![$(\frac{\sqrt[n]{2}-1}{p})_2$ $(\frac{\sqrt[n]{2}-1}{p})_2$](https://dxdy-02.korotkov.co.uk/f/9/8/2/982fa2e2dab649710758fcaffd6c3f5082.png)
равен
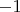
.
Тогда число
![$x^2-y z \sqrt[n]{4}$ $x^2-y z \sqrt[n]{4}$](https://dxdy-04.korotkov.co.uk/f/3/a/5/3a5d695aa3f95eb012eaca43f264200882.png)
сравнимо с квадратом по модулю

.
Этот новый результат явился одной из причин открытия этой темы.
Посмотрим не ошибся ли я, и смогу ли это доказать.