Поиск доказательства, что $x^2-y z \sqrt[n]{4}$ - квадрат

[Феликс Шмидель]

Приступим к изложению доказательства 2-го случая ВТФ.

Пусть ненулевые, взаимно-простые целые числа $x$, $y$ и $z$ удовлетворяют уравнению Ферма: $x^n+y^n+z^n=0$,
где $n$ - нечётное простое число.
Пусть $x y z$ делится на $n$.

Пусть $x$ - нечётное число.
Пусть $(x^2+1)^n-x^{2n}$ не является квадратом.
Последнее утверждение нуждается в доказательстве, но мы пока примем его без доказательства.

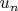
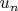
Пусть $u_n$ - генератор мультипликативной группы $\mathbb{Z}_n$, то есть $u_n$ - такое целое число от $1$ до $n-1$, что $u_n^j \not \equiv 1 \mod n$, при $j=1, 2, ..., n-2$.

Пусть $q_1, ..., q_m$ - простые делители числа $(x^2+1)^n-x^{2n}$, которые входят в его разложение на множители в нечётных степенях.

Пусть $p$ - простое число, удовлетворяющее следующим условиям:

1) $p \equiv 3 \mod 4$.

2) $p \equiv u_n \mod n$.

3) $q_1$ является квадратичным невычетом по модулю $p$, а $q_2, ..., q_m$ являются квадратичными вычетами по модулю $p$.

Заметим, что число $(x^2+1)^n-x^{2n}$ нечётное и не делится на $n$ (если одно из чисел $(x^2+1)^n, x^{2n}$ делится на $n$, то другое не делится, а если оба не делятся на $n$, то число $(x^2+1)^n-x^{2n}$ даёт при делении на $n$ остаток $1$).

Условие 3) выполняется, если $p$ даёт остатки при делении на $q_1, q_2, ..., q_m$, которые являются квадратичными вычетами или невычетами, в соответствии с законом квадратичной взаимности для пар $(q_1, p), ..., (q_m, p)$.

Существует бесконечное множество простых чисел $p$, удовлетворяющих условиям 1), 2), 3), в силу китайской теоремы об остатках и теоремы Дирихле о простых числах в арифметической прогрессии.

Среди простых чисел, удовлетворяющих условиям 1), 2), 3), выберем такое $p$, на которое не делится ִִ$x y z$.

Пусть $k$ - целое число, удовлетворяющее сравнению:

$(x^2+1 )^n \equiv y^n z^n 4 (1+k (z^n-y^n)-k^2 y^n z^n) \mod p$.

Запишем это сравнение в виде:

$-k^2 y^n z^n+k (z^n-y^n)+(1-\frac{(x^2+1 )^n}{4 y^n z^n}) \equiv 0 \mod p$.

Дискриминант этого квадратного сравнения равен $(z^n-y^n)^2+4 y^n z^n (1-\frac{(x^2+1 )^n}{4 y^n z^n})=(z^n+y^n)^2-(x^2+1 )^n=x^{2 n}-(x^2+1 )^n$.

Число $(x^2+1 )^n-x^{2 n}$ является квадратичным невычетом по модулю $p$, в силу условия 3).
Следовательно, число $x^{2 n}-(x^2+1 )^n$ является квадратичным вычетом по модулю $p$, в силу условия 1).
Значит существует целое число $k$, удовлетворяющее квадратному сравнению

$(x^2+1 )^n \equiv y^n z^n 4 (1+k (z^n-y^n)-k^2 y^n z^n) \mod p$.

Поскольку любое целое число, сравнимое с $k$ по модулю $p$ также удовлетворяет этому сравнению, то существует бесконечное множество таких $k$.
Выберем такое $k$, чтобы число $4(1+k z^n)(1-k y^n)$ было взаимно-просто с $x$.

Продолжение следует.

[Феликс Шмидель]

Ошибки нет, но мы не можем получить противоречие из равенства

$(\frac{x^2-y z \sqrt[n]{4(1+k z^n)(1-k y^n)}}{p})_2=1$

Для того, чтобы получить противоречие, нужно сначала доказать, что число $x^2-y z \sqrt[n]{4(1+k z^n)(1-k y^n)}$ сравнимо с квадратом в кольце целых алгебраических чисел поля $\mathbb{Q}[\sqrt[n]{4(1+k z^n)(1-k y^n)}]$ по модулю $p$.
Если доказать это, то мы знаем как получить противоречие.

[Феликс Шмидель]

Объясним, как можно получить противоречие.

Мы выбрали простое число $p$ и целое число $k$.
Обозначим: $g_k=\sqrt[n]{4(1+k z^n)(1-k y^n)}$.

Поскольку $x^n+(1+k z^n) y^n+(1-k y^n) z^n=0$, то

$x^{2 n}-y^n z^n g_k^n=((1+k z^n) y^n-(1-k y^n) z^n)^2$.

Запишем это равенство в виде

$(x^2-y z g_k)(x^{2 (n-1)}+x^{2 (n-2)} y z g_k+...+(y z g_k)^{n-1})$ $=$ $((1+k z^n) y^n-(1-k y^n) z^n)^2$.

Сомножители в левой части этого равенства взаимно-просты, поскольку деление второго сомножителя на первый даёт остаток $n (y z g_k)^{n-1}$.
Этот остаток взаимно-прост с $x^2-y z g_k$, поскольку число $x$ взаимно просто с $y z g_k$ и с $n$.
Чтобы $x^2-y z g_k$ было взаимно-просто с $n$, мы с самого начала могли выбрать $x$, не делящийся на $n$ (тогда $y z$ делится на $n$).
Но даже если $x$ делится на $n$, то число $y z g_k$ взаимно-просто с $n$, поскольку взаимно-просто с $x$.

Значит число $x^2-y z g_k$ является квадратом идеала в поле $\mathbb{Q}[g_k]$.
Это число примарное, то есть сравнимое с квадратом по модулю $4$ (поскольку $y z$ делится на $4$).
Согласно закону квадратичной взаимности Гекке для поля $\mathbb{Q}[g_k]$, имеем:

$(\frac{x^2-y z g_k}{p})_2=1$.

Число $p$ неразложимо в поле $\mathbb{Q}[i_n]$, в силу условия 2).
В поле $\mathbb{Q}[g_k]$, число $p$ разлагается в произведение двух простых идеалов $\rho_1$ и $\rho_2$ с нормами $p$ и $p^{n-1}$ соответственно.

Покажем, что $(\frac{x^2-y z g_k}{\rho_1})_2=-1$.

Имеем: $(x^2+1)^n-y^n z^n g_k^n \equiv 0 \mod p$.

Следовательно $((x^2+1)-y z g_k)((x^2+1)^{n-1}+(x^2+1)^{n-2} y z g_k+...+(y z g_k)^{n-1}) \equiv 0 \mod p$.
Поскольку ни один из двух сомножителей в левой части этого сравнения не делится на $p$, то один из них делится на $\rho_1$, а другой на $\rho_2$.
Можно показать, что первый сомножитель делится на $\rho_1$, а второй на $\rho_2$.

Значит $x^2-y z g_k \equiv -1 \mod \rho_1$.

Следовательно $(x^2-y z g_k)^{(p-1)/2} \equiv (-1)^{(p-1)/2} \equiv -1 \mod \rho_1$.

Следовательно $(\frac{x^2-y z g_k}{\rho_1})_2=-1$.

Это противоречит тому, что число $x^2-y z \sqrt[n]{4(1+k z^n)(1-k y^n)}$ сравнимо с квадратом в кольце целых алгебраических чисел поля $\mathbb{Q}[\sqrt[n]{4(1+k z^n)(1-k y^n)}]$ по модулю $p$.

[Феликс Шмидель]

Напомним обозначение: $g_k=\sqrt[n]{4(1+k z^n)(1-k y^n)}$.

Если мы докажем, что число $x^2-y z g_k$ сравнимо с квадратом в кольце целых алгебраических чисел поля $\mathbb{Q}[g_k]$ по модулю $p$, то мы завершим доказательство 2-го случая ВТФ.
Для этого, как мы видели, достаточно найти целое алгебраическое число $v(g_k)$ этого поля, удовлетворяющее двум условиям:

1. Норма числа $v(g_k)$ должна быть квадратичным вычетом по модулю $p$.
2. Квадратичный символ $(\frac{v(g_k)}{p})_2$ должен равняться $-1$.

Следуя Гекке, будем называть число $v(g_k)$ сингулярным, если оно является квадратом идеала поля $\mathbb{Q}[g_k]$.
Если $v(g_k)$ сингулярно, то оно удовлетворяет условию 1.
Мы ограничимся поиском сингулярных чисел $v(g_k)$, удовлятворяющих условию 2.
Предположим таких сингулярных чисел нет, то есть $(\frac{v(g_k)}{p})_2=1$ для всех сингулярных чисел $v(g_k)$.
Согласно теореме 171 на стр. 255 Гекке "Лекции по теории алгебраических чисел", в этом случае существует такое сингулярное положительное число $w(g_k)$, что число $p w(g_k)$ - примарное (то есть сравнимо с квадратом по модулю $4$).
Поскольку $p \equiv 3 \mod 4$, то из этого следует, что число $q w(g_k)$ - примарное для любого простого числа $q$, удовлетворяющего сравнению $q \equiv 3 \mod 4$.
Следовательно, $(\frac{v(g_k)}{q})_2=1$ для всех сингулярных чисел $v(g_k)$, в силу упомянутой теоремы 171 (которая говорит о необходимом и достаточном условии).
Для доказательства 2-го случая ВТФ, нам нужно получить из этого противоречие.

-- Ср мар 16, 2016 12:03:23 --

Если число $p w(g_k)$ - примарное (то есть сравнимо с квадратом по модулю $4$), то его норма - примарное число.
Значит число $p^n$ - примарное.
По-моему, это уже противоречие
Возникает вопрос: в чём ошибка?

[ananova]

Ошибки может и нет. Надеюсь, кто-то сможет проверить, а лучше... Попробовать ещё немного упростить, чтобы ускорить проверку.

[Феликс Шмидель]

Уважаемый ananova, если Вам что-либо в этой теме непонятно, я готов ответить.

-- Пт мар 18, 2016 04:31:18 --

Уважаемые заслуженные участники!

В этой теме я дал условное доказательство 2-го случая ВТФ для произвольного простого показателя $n>2$.
Условное, потому что утверждение, что $(x^2+1)^n-x^{2n}$ не является квадратом принято без доказательства в качестве условия.
Я готов ответить на вопросы по этому доказательству.

[ananova]

(Оффтоп)

Вопросов нет, тк мне понятно только 1/3. Будем ждать уточнений от Вас и коллег.

[Феликс Шмидель]

Феликс Шмидель в сообщении #1107092 писал(а):

Следуя Гекке, будем называть число $v(g_k)$ сингулярным, если оно является квадратом идеала поля $\mathbb{Q}[g_k]$.
Если $v(g_k)$ сингулярно, то оно удовлетворяет условию 1.

Здесь ошибка: число $v(g_k)$ может быть сингулярно и не удовлетворять условию 1.
Так что пока - отбой.

[Феликс Шмидель]

Феликс Шмидель в сообщении #1105687 писал(а):

Найдём такое $k$, что $x^2-y z \sqrt[n]{4(1+k z^n)(1-k y^n)} \equiv -1 \mod p$.

Здесь ошибка: мы нашли такое $k$, что $x^2-y z \sqrt[n]{4(1+k z^n)(1-k y^n)} \equiv -1 \mod \rho_1$.

Феликс Шмидель в сообщении #1105931 писал(а):

Покажем, что $(\frac{x^2-y z g_k}{\rho_1})_2=-1$.

Имеем: $(x^2+1)^n-y^n z^n g_k^n \equiv 0 \mod p$.

Следовательно $((x^2+1)-y z g_k)((x^2+1)^{n-1}+(x^2+1)^{n-2} y z g_k+...+(y z g_k)^{n-1}) \equiv 0 \mod p$.
Поскольку ни один из двух сомножителей в левой части этого сравнения не делится на $p$, то один из них делится на $\rho_1$, а другой на $\rho_2$.
Можно показать, что первый сомножитель делится на $\rho_1$, а второй на $\rho_2$.

Значит $x^2-y z g_k \equiv -1 \mod \rho_1$.

Мы здесь доказываем, что из сравнения $(x^2+1)^n-y^n z^n g_k^n \equiv 0 \mod p$ следует сравнение $x^2-y z g_k \equiv -1 \mod \rho_1$.
Это можно доказать проще: пусть целое положительное число $c$ удовлетворяет сравнению: $x^2-y z c \equiv -1 \mod p$.
Тогда $(x^2+1)^n-y^n z^n c^n \equiv 0 \mod p$, следовательно $c^n \equiv g_k^n \mod p$ (поскольку $(x^2+1)^n-y^n z^n g_k^n \equiv 0 \mod p$).
Мы знаем, что если $c^n \equiv g_k^n \mod p$, то $g_k - c$ делится на $\rho_1$, поэтому из сравнения $x^2-y z c \equiv -1 \mod p$ следует сравнение $x^2-y z g_k \equiv -1 \mod p$, что и требовалось доказать.

-- Пт июн 03, 2016 09:12:48 --

Феликс Шмидель в сообщении #1105123 писал(а):

Число $v(\sqrt[n]{2})$, которое нам нужно взять вместо $\sqrt[n]{2}-1$ должно удовлетворять двум условиям:

1. Норма числа $v(\sqrt[n]{2})$ должна быть квадратичным вычетом по модулю $p$.
2. Квадратичный символ $(\frac{v(\sqrt[n]{2})}{p})_2$ должен равняться $-1$.

Если такое число $v(\sqrt[n]{2})$ существует, то $x^2-y z \sqrt[n]{4}$ сравнимо с квадратом по модулю $p$.

Я думаю, что такое число существует, но доказать это пока не могу.

Для того, чтобы закончить доказательство ВТФ, нужно доказать существование числа $v(g_k)$, удовлетворяющего двум условиям:

1. Норма числа $v(g_k)$ должна быть квадратичным вычетом по модулю $p$.
2. Квадратичный символ $(\frac{v(g_k)}{p})_2$ должен равняться $-1$.

-- Пт июн 03, 2016 09:34:49 --

Из существования такого числа $v(g_k)$ следовало бы то, что $x^2 - y z g_k$ сравнимо квадратом по модулю $p$, что противоречило бы доказанному нами сравнению: $x^2-y z g_k \equiv -1 \mod \rho_1$.

[Феликс Шмидель]

Если бы нам удалось доказать, что $x^2 - y z g_k$ сравнимо квадратом по модулю $\rho_1$, то из этого следовало бы то, что $x^2 - y z g_k$ сравнимо квадратом по модулю $p$, поскольку $(\frac{x^2-y z g_k}{p})_2=1$:

Феликс Шмидель в сообщении #1105931 писал(а):

Значит число $x^2-y z g_k$ является квадратом идеала в поле $\mathbb{Q}[g_k]$.
Это число примарное, то есть сравнимое с квадратом по модулю $4$ (поскольку $y z$ делится на $4$).
Согласно закону квадратичной взаимности Гекке для поля $\mathbb{Q}[g_k]$, имеем:

$(\frac{x^2-y z g_k}{p})_2=1$.

Значит, чтобы закончить доказательство ВТФ, достаточно также доказать, что $(x^2 - y z g_k)^{(p-1)/2} \equiv 1 \mod \rho_1$.

[Феликс Шмидель]

Вместо $(\frac{x^2-y z g_k}{\rho_1})_2=1$ достаточно доказать, что $(\frac{x^2-y z g_k}{\rho_2})_2=1$.
Пусть $(x^2-y z g_k)^{(p^{n-1}-1)/2}=b_0+b_1 g_k+b_2 g_k^2+...+b_{n-1} g_k^{n-1}$, где $b_0, b_1, ..., b_{n-1}$ -целые числа.
Пусть $s$ - такое целое положительное число, что $s^n \equiv g_k^n \mod p$.
Тогда $(x^2-y z s i_n)^{(p^{n-1}-1)/2} \equiv b_0+b_1 (s i_n)+b_2 (s i_n)^2+...+b_{n-1} (s i_n)^{n-1} \mod p$.
Поскольку $p$ - простое число в кольце $\mathbb{Z}[i_n]$, то левая часть этого сравнения сравнима либо с $1$, либо с $-1$ по модулю $p$.
Значит либо
$b_0-1 \equiv b_1 s \equiv b_2 s^2 \equiv ... \equiv b_{n-1} s^{n-1} \mod p$
либо,
$b_0+1 \equiv b_1 s \equiv b_2 s^2 \equiv ... \equiv b_{n-1} s^{n-1} \mod p$.
Кроме того $(x^2-y z s)^{(p^{n-1}-1)/2} \equiv b_0+b_1 s+b_2 s^2+...+b_{n-1} s^{n-1} \mod p$.
Нетрудно показать, что правая часть этого сравнения сравнима с $1$ по модулю $p$.
Если $b_0-1 \equiv b_1 s \equiv b_2 s^2 \equiv ... \equiv b_{n-1} s^{n-1} \mod p$, то
$b_0 \equiv 1 \mod p$, $b_1 \equiv 0 \mod p$, ... $b_{n-1} \equiv 0 \mod p$.
В этом случае $(x^2-y z g_k)^{(p^{n-1}-1)/2} \equiv 1 \mod p$, следовательно $(\frac{x^2-y z g_k}{\rho_2})_2=1$, что и требовалось.
Пусть теперь $b_0+1 \equiv b_1 s \equiv b_2 s^2 \equiv ... \equiv b_{n-1} s^{n-1} \mod p$.
Поскольку $(b_0-1)+b_1 s+b_2 s^2+...+b_{n-1} s^{n-1} \equiv 0 \mod p$, то $n b_1 s \equiv 2 \mod p$.
Итак, в этом случае, имеем:
$b_0+1 \equiv b_1 s \equiv b_2 s^2 \equiv ... \equiv b_{n-1} s^{n-1} \equiv 2/n \mod p$.
Вряд ли эти сравнения выполняются при заданных $x, y, z$.
Но можно добавить ещё сравнение: $(x^2-y z g_k)^{(p^{n-1}-1)/2} \equiv -1 \mod \rho_2$ и попробовать получить противоречие.

-- Пт июн 03, 2016 15:33:20 --

Из сравнений $b_0+1 \equiv b_1 s \equiv b_2 s^2 \equiv ... \equiv b_{n-1} s^{n-1} \equiv 2/n \mod p$ и
равенства $(x^2-y z g_k)^{(p^{n-1}-1)/2}=b_0+b_1 g_k+b_2 g_k^2+...+b_{n-1} g_k^{n-1}$ получим:

$(x^2-y z g_k)^{(p^{n-1}-1)/2} \equiv -1+(2/n) (1+(g_k/s)+(g_k/s)^2+...+(g_k/s)^{n-1})$ по модулю $p$.

Из этого сравнения следует сравнение $(x^2-y z g_k)^{(p^{n-1}-1)/2} \equiv -1 \mod \rho_2$, поэтому последнее сравнение ничего не даёт.
Проверим ещё сравнение $(x^2-y z g_k)^{(p^{n-1}-1)/2} \equiv 1 \mod \rho_1$.
Оно следует из того, что $g_k/s \equiv 1 \mod \rho_1$.

Но из сравнения:

$(x^2-y z g_k)^{(p^{n-1}-1)/2} \equiv -1+(2/n) (1+(g_k/s)+(g_k/s)^2+...+(g_k/s)^{n-1})$ по модулю $p$

можно попробовать получить противоречие.

[Феликс Шмидель]

Вернёмся к нашему рассуждению:

Феликс Шмидель в сообщении #1107092 писал(а):

Следуя Гекке, будем называть число $v(g_k)$ сингулярным, если оно является квадратом идеала поля $\mathbb{Q}[g_k]$.
Если $v(g_k)$ сингулярно, то оно удовлетворяет условию 1.
Мы ограничимся поиском сингулярных чисел $v(g_k)$, удовлятворяющих условию 2.
Предположим таких сингулярных чисел нет, то есть $(\frac{v(g_k)}{p})_2=1$ для всех сингулярных чисел $v(g_k)$.
Согласно теореме 171 на стр. 255 Гекке "Лекции по теории алгебраических чисел", в этом случае существует такое сингулярное положительное число $w(g_k)$, что число $p w(g_k)$ - примарное (то есть сравнимо с квадратом по модулю $4$).
Если число $p w(g_k)$ - примарное (то есть сравнимо с квадратом по модулю $4$), то его норма - примарное число.
Значит число $p^n$ - примарное.
По-моему, это уже противоречие.

Я перечитал и снова вижу, что это имеет смысл.
Если есть ошибка, может быть можно исправить.
Поэтому я решил дополнительно порассуждать на эту тему.

Основанием для этого рассуждения является обращение теоремы 166 на стр. 245 учебника Гекке.
После формулировки этой теоремы, следует утверждение: "Что эта теорема допускает обращение будет доказано лишь в следующем параграфе."
Обратная теорема в применении к нашему случаю означает то, что существует делитель единицы или сингулярное число $v(g_k)$ (то есть являющееся квадратом идеала), для которого $(\frac{v(g_k)}{p})_2=-1$.
Оставим пока вопрос о доказательстве этого утверждения, и посмотрим, можно ли исходя из него закончить наше доказательство ВТФ.

[Феликс Шмидель]

Заметим, что либо $x^2-yz g_k$, либо $-(x^2-yz g_k)$ сравнимо с квадратом по модулю $p$ в силу того, что $(\frac{x^2-yz g_k}{p})_2=1$.
Заметим также, что при перемене знака числа $v(g_k)$ норма также меняет знак, что даёт возможность получить норму, являющуюся квадратичным вычетом по модулю $p$ (если $p \equiv 3 \mod 4$).
А квадратичный символ $(\frac{v(g_k)}{p})_2$ при перемене знака числа $v(g_k)$ не меняется (так как $p$ является произведением двух простых идеалов).
Поэтому не обязательно брать сингулярное $v(g_k)$, достаточно, чтобы $(\frac{v(g_k)}{p})_2=-1$, а норму числа $v(g_k)$ можно
сделать квадратичным вычетом по модулю $p$ переменой знака.
В связи с этим нужно ещё раз проверить правильность леммы 7A, поскольку простота доказательства становится подозрительной.

-- Вс июн 05, 2016 22:48:23 --

Феликс Шмидель в сообщении #1129331 писал(а):

А квадратичный символ $(\frac{v(g_k)}{p})_2$ при перемене знака числа $v(g_k)$ не меняется (так как $p$ является произведением двух простых идеалов).

Это утверждение ошибочно. Квадратичный символ $(\frac{v(g_k)}{p})_2$ меняет знак при перемене знака числа $v(g_k)$ , так как $(\frac{-1}{\rho_1})_2=(-1)^{(p-1)/2}<0$, а $(\frac{-1}{\rho_2})_2=(-1)^{(p^{n-1}-1)/2}>0$.

Получается, что всё это сообщение ошибочно, и неверно, что либо $x^2-yz g_k$, либо $-(x^2-yz g_k)$ сравнимо с квадратом по модулю $p$.

[Феликс Шмидель]

Теперь понятно, что просто найти такой делитель единицы или сингулярное число $v(g_k)$ (то есть являющееся квадратом идеала), для которого $(\frac{v(g_k)}{p})_2=-1$.
Достаточно взять $v(g_k)=-1$ или взять любое сингулярное число $v(g_k)$ и помножить его (если $(\frac{v(g_k)}{p})_2=1$) на $-1$.
Заметим, что умножение сигулярного числа на делитель единицы может быть единственной опцией, потому что если взять два сингулярных числа $\alpha=I^2$ и $\beta=J^2$, где идеалы $I$ и $J$ принадлежат одному классу идеалов, то $(\frac{\alpha}{p})_2=(\frac{\beta}{p})_2$.
Таким образом, обращение теоремы 166 на стр. 245 учебника Гекке доказывается совсем просто.
Но для нашего доказательства нужно найти такое сингулярное число $v(g_k)$, чтобы не только $(\frac{v(g_k)}{p})_2=-1$, но чтобы ещё норма числа $v(g_k)$ была положительной (в этом случае она равна квадрату, а иначе минус квадрату).
Поэтому мое замечание:

Феликс Шмидель в сообщении #1107967 писал(а):

Здесь ошибка: число $v(g_k)$ может быть сингулярно и не удовлетворять условию 1.

было правильным.

-- Пн июн 06, 2016 07:12:48 --

Если помножить $p$ на сингулярное число (являющееся квадратом идеала), то нельзя получить примарное и вполне положительное число (поскольку $p \equiv 3 \mod 4$), поэтому существует сингулярное число $v(g_k)$, для которого $(\frac{v(g_k)}{p})_2=-1$ (как мы видели и в силу теоремы 171 на стр. 255 учебника Гекке).

Но таким умножением можно получить примарное (но не вполне положительное число) (умножая сингулярный множитель на $-1$),
поэтому не существует вполне положительного сингулярного числа $v(g_k)$, для которого $(\frac{v(g_k)}{p})_2=-1$ (в силу теоремы 173 на стр. 255 учебника Гекке).

Значит в обсуждаемом нами методе доказательства, мы не можем рассчитывать на вполне положительные сингулярные числа.

[Феликс Шмидель]

Идея в начале этой темы основана на заблуждении.

Феликс Шмидель в сообщении #1104525 писал(а):

Пусть $p$ - такое простое число, что квадратичный символ $(\frac{\sqrt[n]{2}-1}{p})_2$ равен $-1$.

Дело в том, что квадратичный символ $(\frac{\sqrt[n]{2}-1}{p})_2$ всегда равен $1$, поскольку
$(\frac{\sqrt[n]{2}-1}{\rho_1})_2=(\frac{\sqrt[n]{2}-1}{\rho_2})_2$.
Это прямо следует из леммы 6A: $s-1$ является квадратичным вычетом по модулю $p$ тогда и только тогда, когда $s i_n-1$ сравнимо с квадратом в кольце $\mathbb{Z}[i_n]$ по модулю $p$.