При описании поведения квантовой частицы в одномерной потенциальной яме используется волновая функция
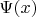
(1) из гильбертова пространства

Для описания поведения трех частиц используется функция

(2), а для описания одной частицы в 3-мерной яме используется функция

(3). В принципе, в (2) и в (3) - функции от трех переменных, а само гильбертово пространство

- тензорное произведение одномерных пространств. Для описания 3-мерного поведения

частиц нужно

. Например, для описания 2 частиц нужно

, а для описания трех уже нужно

. И если для одной частицы как-то можно представить пси-функцию не как математическую абстракцию, а как нечто физическое "в этом месте", то для

это проблема. Далее, если 2 частицы рядом, а третья далеко (и нам не мешает), то каким образом

редуцируется в

? А ведь далеко-далеко есть 4,5,

-я частицы и тогда для полного описания нужно

... Какое из гильбертовых пространств "правильное"? Или никакое, все они "проекции" неизвестного? правильного описания... Давно читал книгу Эмха про

-алгебры, где гильбертовы пространства служили для представления алгебр. Но потом это направление то ли заглохло, то ли стало неактуальным.
Для двух "наших" близких частиц и "чужой" далекой сделаем так: разложим

и, пока чужая частица далеко, будем считать, что

, при приближении третьей перейдем к

, а когда "чужая частица удалится, снова вернемся к

. Увы, простое произведение двух функции после разлета, вообще говоря, не получится и для описания подсистем (нашей и чужой) надо будет использовать матрицу плотности. Чужая частица улетела, но ее пагубное влияние на чистое состояния нашей пары осталось (и наоборот - теперь состояние улетевшей частицы не может описываться чистой пси-функцией

т.е. вектором в

). Имхо, именно поэтому разговоры про кота Шредингера и смешанное состояние живой-мертвый беспочвенны. Кот излучил такую уйму фотонов ("чужих" далеких частиц), что его собственные состояния не могут интерферировать между собой и состояние кота должно описываться матрицей плотности.
Интуитивно кажется, что частица не знает, в каком гильбертовом пространстве находится ее состояние и какой пси-функцией / матрицей оно описывается. Но каким математическим аппаратом это адекватно выразить? Диаграммами Фейнмана (там расходимости) или интегралами по траекториям (увы, мне не вполне ясно, что это такое с формализованной точки зрения, когда есть взаимодействие)? Может диаграммы - не просто картинки для расчетов, а какое-то отражение реального поведения? Частица как бы "прощупывает" окружение и формируется ее новое "состояние"? И потом это "состояние" находит отражение в пси-функциях (матрицах) тех подсистем, куда входит (входила) частица. Возможно, для кого-то [почти] все вышесказанное звучит, как бред, но все же...