доказать монотонность неявной функции

[ozhezhka]

Помогите, пожалуйста, доказать, что неявная функция $t(p)$, задаваемая уравнением

$\frac{2-(1-p r)^{N+1}-(1-p\overline{r})^{N+1}}{p(N+1)}= 1-r(1-(1-p r)^N)e^{-\mu_1 t}-\overline{r}(1-(1-p\overline{r})^N)e^{-\mu_2 t}$

строго возрастает по $p$ для всех натуральных $N>1$ , действительных $0<p\le 1, 0 \le r\le 1, \overline{r}=1-r, \mu_1, \mu_2>0$.

В лоб через производную получается огромное выражение, знак которого сложно оценить. То же и с матиндукцией. Может кто-то подскажет идею?

[DeBill]

ИДЕЯ: А давайте лучше докажем, что она убывет!
Ну хотя бы для частного случая $r=\frac{1}{2}, N=2, \mu_1 =\mu_2 = 1$.
Прямые выкладки дают

$e^{-t}= \frac{6-p}{3\cdot(4-p) }$

И правда, убывает...

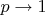
ЗЫ Обратите внимание на то, что при $p=0$ (в пределе, конечно) получается $t=\ln2$. И в ощем случае тоже получается, что:1) при $p=0$, $t$ нулю не равно 2) $t(p) $ убывает при малых $p$. Посмотрите ещё предельные случаи $r=1,p\to 0 $ (или $p\to1$ ) - чтобы понять, что у Вас вообще происходит.
А задачка-то - из теории вероятностей?

[ozhezhka]

да, убывает. В задаче надо доказать убывание. Опечатка. Exp(-t(p)) возрастает.

задача из теории массового обслуживания

если в Mathcad например построить график то реально убывает. Для N=1 получается константа не зависящая от p. Для 2 можно через производную показать. То есть база индукции есть. А вот для произвольного уже сложности.

[ozhezhka]

вопрос снимается.
спасибо всем, кто пытался помочь

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);


Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.