Нестандартные задачи

[Юстас]

Kid Kool писал(а):

Юстас писал(а):

$x=7t+1, \ t=4p$

У тебя, судя по дальнейшим выкладкам, получается $x = 4p+1$, а при чем тут t и делимость на 7 - не понятно. Ну да ладно

Исправил предыдущий пост.

[Kid Kool]

Юстас писал(а):

$16p^3+12p^2+5p+1=8^k$. Это тоже неразрешимо по модулю 7.

Ну как же неразрешимо, p делится на 7 и делов.

[juna]

Trius писал(а):

2) Решить в натуральных числах $x^3+2x+1=2^n$

Если существует решение при $n>2$, то
1) $n\equiv 0 \mod 3\to\exists y: x^3+2x+1=y^3\to2x+1=(y-x)(y^2+yx+x^2)$ - невозможно;
2) $n\equiv 1 \mod 3\to\exists y: x^3+2x+1=2y^3$ - невозможно;
3) $n\equiv 2 \mod 3\to\exists y: x^3+2x+1=4y^3$ - невозможно.

student писал(а):

Покажите, что для натуральных чисел $x,y,z$ выражение
$(xy+1)(yz+1)(zx+1)$ будет точным квадратом, только в том случае если каждое из трех чисел $xy+1,\ yz+1,\ zx+1$ были точными квадратами.

см. здесь

[Юстас]

juna писал(а):

3) $n\equiv 2 \mod 3\to\exists y: x^3+2x+1=4y^3$ - невозможно.

Можно подробнее?

[juna]

Когда я это писал, находился во власти иллюзии. Сейчас вижу, что 2), 3) нужно доказывать.
Т.е. вопрос остается открытым.

[Юстас]

2) доказывается по модулю 7, а 3) я тоже не знаю.

[Юстас]

Trius писал(а):

Доказать, что существует бесконечно много таких пар целых чисел $a$ и $b$, для которых $a^{2006}+1$делится на $b$, а $b^{2006}+1$делится на $a$.

Kid Kool писал(а):

Существует бесконечно много b, таких что $3b^2 = t^2 + 1$ (уравнение Пелля). Для такого b найдется целое a, такое что $a^2 + b^2 + 1 = 4ab$ (a = 2b+t). a, b - искомые.

Кажется, уравнение $3b^2=t^2+1$ не имеет решений.

[Kid Kool]

Юстас писал(а):

Trius писал(а):

Доказать, что существует бесконечно много таких пар целых чисел $a$ и $b$, для которых $a^{2006}+1$делится на $b$, а $b^{2006}+1$делится на $a$.

Kid Kool писал(а):

Существует бесконечно много b, таких что $3b^2 = t^2 + 1$ (уравнение Пелля). Для такого b найдется целое a, такое что $a^2 + b^2 + 1 = 4ab$ (a = 2b+t). a, b - искомые.

Кажется, уравнение $3b^2=t^2+1$ не имеет решений.

Ты прав, наверное.

Можно брать b такие, что $5b^2 = t^2 + 4$. Тогда для $a = \frac {3b + t} 2$ будет выполнено $a^2 + b^2 + 1 = 3ab$, что тоже подходит.

[нг]

Задача Slash отделена.

Задача Slash повторно отделена.

нг:

Slash
Пожалуйста, следуйте правилам: редактируйте уже существующее сообщение, а не помещайте новое.

[student]

Пусть $a,b,c$-целые числа удовлетворяющие условию $0<a<c-1$ и $1<b<c$. Для каждого $k,\ 0\le k\le a$, пусть $r_k,\ 0\le r_k<c$, есть остаток от деления $kb$ на $c$. Докажите, что множества $\{r_0,r_1,\ldots , r_a\}$ и $\{0,1,\ldots, a\}$ различны.

[bobo]

Обозначим второе множество через $A$. Предположим, что оно совпадает с первым множеством, тогда, очевидно, $c$ и $b$ взаимнопросты ( иначе единица не попадет в $A$). Пусть $lb < c < (l+1)b$, это означает, что $lb$ принадлежит $A$ и $c-b < lb$ также содержится в $A$. Но последнее, т.к. $b$ и $c$ взаимнопросты, возможно лишь при $ k = c-1$ - противоречие.

[Trius]

Доказать или опровергнуть существования многочлена с целыми коэффициентами, корнем которого было б число $\sqrt[3]{2}+\sqrt{1+\sqrt{2}}$

[Профессор Снэйп]

Trius писал(а):

Доказать или опровергнуть существования многочлена с целыми коэффициентами, корнем которого было б число $\sqrt[3]{2}+\sqrt{1+\sqrt{2}}$

Сумма алгебраических чисел (равно как разность, произведение и частное) является алгебраическим числом.

Число $\sqrt[3]{2}$ является корнем уравнения

$$ x^3-2=0 $$

Число $\sqrt{1+\sqrt{2}}$ является корнем уравнения

$$ (x^2-1)^2-2=0 $$

Таким образом, число $\sqrt[3]{2}+\sqrt{1+\sqrt{2}}$ является корнем уравнения с целыми коэффициентами.

P. S. Выписать само уравнение не трудно, но в задаче этого не требуется.

[maxal]

bobo писал(а):

Обозначим второе множество через $A$. Предположим, что оно совпадает с первым множеством, тогда, очевидно, $c$ и $b$ взаимнопросты ( иначе единица не попадет в $A$). Пусть $lb < c < (l+1)b$, это означает, что $lb$ принадлежит $A$

С чего бы это? Такое можно утверждать, только если $l\leq a$, но это ниоткуда не следует.

Добавлено спустя 2 часа 25 минут 56 секунд:

student писал(а):

Пусть $a,b,c$-целые числа удовлетворяющие условию $0<a<c-1$ и $1<b<c$. Для каждого $k,\ 0\le k\le a$, пусть $r_k,\ 0\le r_k<c$, есть остаток от деления $kb$ на $c$. Докажите, что множества $\{r_0,r_1,\ldots , r_a\}$ и $\{0,1,\ldots, a\}$ различны.

Предположим, противное, то есть что $\{r_0,r_1,\ldots , r_a\}=\{0,1,\ldots, a\}=[0,a]$.
Тогда, в частности, $1=r_d$ для некоторого $d\leq a$. Понятно, что $d\equiv b^{-1}\pmod{c}$ и $r_{k+d}=r_k+1$ для любого $k$.

Разделим $a$ на $d$ с остатком: $a = qd + p$, где $0\leq q<a$ и $0\leq p<d$.
Тогда целочисленный отрезок $[0,a]$ распадается на непересекающиеся отрезки (все арифметические операции производятся по модулю $c$):

$$I_0 = \{ r_0=0,\ r_d = 1,\ \dots, r_{qd}=q \} = [0,q]$$

$$I_1 = \{ r_1=b,\ r_{1+d} = b+1,\ \dots, r_{1+qd}=b+q \} = [b,b+q]$$

$$\dots$$

$$I_p = \{ r_p=pb,\ r_{p+d} = pb+1,\ \dots, r_{p+qd}=pb+q \} = [pb,pb+q]$$

$$I_{p+1} = \{ r_{p+1}=(p+1)b,\ r_{p+1+d} = (p+1)b+1,\ \dots, r_{p+1+(q-1)d}=(p+1)b+q-1 \} = [(p+1)b,(p+1)b+q-1]$$

$$\dots$$

$$I_{d-1} = \{ r_{d-1}=(d-1)b,\ r_{d-1+d} = (d-1)b+1,\ \dots, r_{d-1+(q-1)d}=(d-1)b+q-1\} = [(d-1)b,(d-1)b+q-1]$$

Так как числа $r_k=kb$ для $0<k<d$ (т.е. в количестве $d-1$ штуки) являются началами отрезков, то числа $r_k-1=kb-1$ обязаны быть концами отрезков. Так как $(r_{k+1}-1)-(r_{k}-1)=b$, то должна существовать последовательность из $d-1$ концов отрезков, где расстояние между соседними членами равно $b$. Как нетрудно видеть, мы можем расположить все отрезки в виде последовательности

$$I_{p+1}, I_{p+2}, \dots, I_{d-1}, I_0, I_1, \dots, I_p,$$

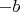
где прибавление $b$ концу одного отрезка дает конец следующего. Далее, один из концов равен $(d-1)b-1=-b$ ($=c-b$), и прибавление $b$ к нему дает $0$, что не является концом никакого отрезка. Поэтому $-b$ должно быть концом отрезка $I_p$, то есть $-b = pb+q$ или $(p+1)b+q=0$. Но в этом случае конец отрезка $I_{p+1}$ равен $c-1$, что невозможно в силу условия $a<c-1$. Поэтому отрезка $I_{p+1}$ не существует, то есть $p=d-1$. Но и в этом случае получается невозможное соотношение $0=(p+1)b+q=db+q=1+q$, то есть $q=c-1>a$. Полученное противоречие доказывает, что $\{r_0,r_1,\ldots , r_a\}\ne \{0,1,\ldots, a\}$.

[Kid Kool]

maxal писал(а):

С чего бы это? Такое можно утверждать, только если $l\leq a$, но это ниоткуда не следует.

Если $l > a$, то $ab < lb < c$, т.е. все остатки $r_k$ на самом деле равны kb. Тогда получается один вариант - $b = 1$, а это по условию невозможно.