Артамонов Ю.Н. писал(а):
Приведу схему доказательства:
1. Нужно показать, что

;
2.

.
Тогда очевидно, что

, т.к. при

получим ровно

.
Осталось доказать п.1 и п. 2.

Анализ сформулированных пунктов приводит к необходимости отдельного рассмотрения двух случаев:
в виду симметрии положим

,
Случай 1.

;
Случай 2.

.
Докажем справедливость неравенства для случая 1.
1. Докажем п.1.

. После преобразований имеем

. Рассмотрим функцию

. Она принимает неотрицательные значения, когда

, действительно, после преобразований имеем

- верно при

. Поскольку у нас для этого случая

, то

и

, а

имеет больший порядок малости, т.к. здесь делим на самое большое

и умножаем на самое малое

.
2. Докажем п.2. Здесь нам нужно доказать, что функция

монотонная, выпуклая вниз, начиная с некоторого

. Тогда становится ясно, что она ограничена снизу
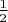
, т.к. при

она равна

. Функция терпит три разрыва, можно показать, что в точке крайнего правого разрыва плюс нуль функция уходит в плюс бесконечность (хотя это и непринципиально для доказательства). Поскольку

имеет конечное число точек экстремума, то ясно, что, начиная с некоторого

, она будет монотонной. Докажем, что она будет монотонно убывать. Рассмотрим функцию

и выясним условие, при котором она выпукла вниз при положительном

. Имеем

. После преобразований получаем требование

. Таким образом, в случае 1 две компоненты функции

выпуклы вниз. Для того, чтобы показать, что

выпукла вниз, достаточно убедиться, что

. Имеем

. В виду изложенного, здесь

,

, а

имеет в сравнении с ними больший порядок малости, т.к. умножаем на меньшее, делим на большее. ч.т.д.