Задачи на теорию вероятности

[ewert]

rabbit-a в сообщении #1071626 писал(а):

потому что порядок важен все-таки(!)

Он важен или не важен ровно постольку, поскольку он важен или неважен в знаменателе. Т.е. попросту (в данном случае) буковки вверху и внизу должны быть одинаковыми.

[Lia]

rabbit-a
Замечание за неоформление $\TeX$ом, post1071617.html#p1071617
Оформлено, ибо лень нести в Карантин. В следующий раз мне будет лень нести обратно, обещаю.

[rabbit-a]

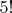
Ewert, все еще не могу понять какого множителя не хватает в числителе! Вроде бы я все учел, если умножить на число перестановок (или что то же самое взять в знаменателе число сочетаний) $5!$, то вероятность будет больше 1, чего быть не может. Да и когда мы используем правило произведения, это ведь уже предполагает, что множества содержащие одинаковые элементы но в разно м порядке считаются различными.
$p=\frac{52\cdot 3\cdot (52-4)\cdot(52-8)\cdot(52-12)}{A_{52}^5}=\frac{176}{4165}$
$52-4$ - это число карт другого достоинства, нежели две предыдущие
$52-8$ - это число карт другого достоинства, чем три предыдущие
$52-12$- это число карт другого достоинства, чем все предшествующие
откуда там быть еще какому-то множителю?
Lia, Вы бы сказали я сам бы исправил

[Lia]

(Оффтоп)

Время редактирования ограничено.

[provincialka]

rabbit-a
А что, одинаковые карты непременно первыми достают? Может ли так быть, что совпадают, скажем, 3-ья карта и 5-ая? Раз уж вы учитываете порядок.

[rabbit-a]

Да, конечно, может. Но тогда получается что нужно умножить на число перестановок $P_5=5 !=120$ и вероятность получается больше единицы

[provincialka]

Почему перестановок?
Нет, не так. Надо перечислить , на каких местах могут оказаться пары одинаковых карт. Вернее, выяснить, сколько таких расположений возможно.

[rabbit-a]

т.е. умножить на $C_5^2=10$? а почему нужно переставлять именно пары карт а не каждую с каждой?

[provincialka]

Не надо "переставлять". Вот, например, вы считаете варианта, когда "одинаковые" карты оказались на 1 и 2 месте. Потом -- варианты, когда "одинаковые" -- на 1 и 3 местах. Сколько их? Да столько же, как в первом подсчете. И т.д.

[rabbit-a]

Хорошо, т.е. правильный ответ $\frac{176\cdot C_5^2}{4165}=\frac{352}{833}$?
И как Вы считаете способен семиклассник решить такую задачу?

[ewert]

(Оффтоп)

rabbit-a в сообщении #1072084 писал(а):

И как Вы считаете способен семиклассник решить такую задачу?

А это уж не к нам вопрос. Вернее, не в эту ветку. Это в "Вопросы преподавания".

[rabbit-a]

(Оффтоп)

Хорошо, спасибо большое всем за разбор задачи и обсуждение