Закон больших чисел

[Diom]

Gordmit писал(а):

Ну так там же, насколько я понял, Гнеденко показывает, чем отличается ЗБЧ от УЗБЧ: в первом утверждается, что для достаточно большого $n$ вероятность одного единственного неравенства

$$\left|\frac1n\sum\xi_k-\frac1n\sum\mathsf{M}\xi_k\right|<\varepsilon$$

может быть сделана больше $1-\eta$ при любом $\eta>0$, а во втором - что вероятность одновременного выполнения целых $s$ неравенств (причем s любое):

$$\max_{n_0\leqslant n\leqslant n_0+s}\left|\frac1n\sum\xi_k-\frac1n\sum\mathsf{M}\xi_k\right|<\varepsilon$$

может быть сделана выбором $n_0$ сколь угодно близкой к 1.
Может в этом отличие и состоит?

В чем отличие УЗБЧ от ЗБЧ я уже понял, вопрос теперь встал в другом - в том насколько формулировка УЗБЧ приведенная в Гнеденко соответствует другой формулировке УЗБЧ, где требуется сходимость "почти наверно". По моему они не равносильны.

[GSav]

Скажите пожалуйста, есть ли какие-либо дополнительные сведения (или способ оценить) об \varepsilon в неравенстве

$$\left|\frac1n\sum\xi_k-\frac1n\sum\mathsf{M}\xi_k\right|<\varepsilon$$

(считая, что берется конечное n>n_0).
Я нашел только это: http://en.wikipedia.org/wiki/Sample_size

[--mS--]

GSav писал(а):

Скажите пожалуйста, есть ли какие-либо дополнительные сведения (или способ оценить) об \varepsilon в неравенстве

$$\left|\frac1n\sum\xi_k-\frac1n\sum\mathsf{M}\xi_k\right|<\varepsilon$$

(считая, что берется конечное n>n_0).
Я нашел только это: http://en.wikipedia.org/wiki/Sample_size

Вопрос непонятен. Никакого $\varepsilon$, удовлетворяющего этому неравенству для произвольных (даже независимых и одинаково распределённых) случайных величин при заданном $n$, вообще говоря, не существует. Уточните, пожалуйста, что именно требуется.

[GSav]

Спасибо за Ваш ответ. Я нашел как свести проблему к теореме Чебышева.
Но все-таки интересно понять -- а если количество случайных величин -- большая, но конечная величина, то можно ли утверждать, что приведенный выше модуль разности будет заведомо меньше некоторой величины или, например, будет порядка O(n^m), где m < 1.

[--mS--]

"Заведомо меньше" - вообще говоря, нет. Ну возьмите сумму независимых слагаемых со стандартным нормальным распределением. При совершенно любом $n$ под модулем стоит нормально распределённая случайная величина с нулевым матожиданием и дисперсией $1/n$. Поэтому модуль неограничен: какое бы ни было $\varepsilon>0$, вероятность этому модулю быть больше него положительна (и лишь стремится к нулю с ростом $n$).

Может быть, Вы всё же попробуете описать, что именно нужно? Потому что неравенство Чебышёва точно так же ничего не может дать для Вашего вопроса: по неравенству Чебышёва можно лишь оценить снизу вероятность неравенства $\left|\frac{\xi_1+\ldots+\xi_n}{n}- \frac{\mathsf E\xi_1+\ldots+\mathsf E\xi_n}{n}\right|<\varepsilon$.

[Henrylee]

Diom писал(а):

В книге Гнеденко нашел ещё одну формулировку УЗБЧ:
Последовательность случайных величин подчиняется узбч, если, каковы бы не были

\[ \varepsilon > 0,{\rm{ }}\eta {\rm{ > 0}} \]

можно указать такое

\[ {\rm{n}}_{\rm{0}} \]

, что для любого s и всех n удовлетворяющих неравенствам

\[ n_0 \le n \le n_0 + s \]

, вероятность неравентсва

\[ \mathop {\max }\limits_{n_0 \le n \le n_0 + s} \left| {\frac{1}{n}\sum\limits_{i = 1}^n {\xi _i } - \frac{1}{n}\sum\limits_{i = 1}^n {M\xi _i } } \right| < \varepsilon \]

больше, чем

\[ 1 - \eta \]

Насколько эта формулировка соответствует приведенной ранее? Мне кажется, она более слабая ведь в предыдущей формулировке говорилось о том что это неравенство должно выполнятся с вероятностью 1, а здесь с вероятностью сколь угодно близкой к 1.

Попробуйте доказать, что

$$ \bigcup\limits_{n_0=1}^\infty\bigcap\limits_{s=1}^\infty\left\{\max\limits_{n_0\leqslant n\leqslant n_0+s}a_n<\varepsilon\right\}\subseteq\left\{\overline{\lim}a_n\leqslant\varepsilon\right\} $$

где $a_n$ понятно что. Отсюда получите нужное включение.

[--mS--]

Henrylee писал(а):

Попробуйте доказать, что

Скорее всего через 13 месяцев после исходного сообщения у автора вопрос отпал сам собой

[Henrylee]

На дату не посмотрел

[GSav]

Уважаемый --mS--, искренне признателен Вам за прояснение. Конечно-же вопрос некорректен -- я не учел, что неравенство $\left|\frac{\xi_1+\ldots+\xi_n}{n}- \frac{\mathsf E\xi_1+\ldots+\mathsf E\xi_n}{n}\right|<\varepsilon$ выполняется с вероятностью 1 для сколь угодно малого \varepsilon лишь в пределе, когда количество случайных величин стремится к бесконечности.

Сейчас все честно -- имеется распределение Бернулли, дисперсии ограничены. Количество независимых случайных величин стремится к бесконечности. Численные эксперименты прошли успешно.

Ушел освежать в памяти теор.вер.

[--mS--]

Ну может ещё ЦПТ посмотреть, вдруг она будет здесь полезна? Эк тщательно Вы скрываете, что именно хотите получить

[GSav]

--mS-- писал(а):

Эк тщательно Вы скрываете, что именно хотите получить

Совсем нет, отнюдь. Просто для этого форума задача может показаться слишком детской, да и латех для меня сложен -- все никак не перейду на него с OpenOffice.
Вот в чем задача. Имеем
x=\sum\limits_{i=1}^{f(x)} a_i (*)
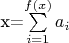
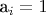
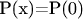
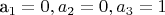
где x - натуральное число. f(x) для определенности считаем также натуральным числом, a - случайные величины, принимающие значения 0 и 1, причем известна вероятность 1 -- она зависит от x(i). Т.е. ведет себя эта конструкция так: x(i=0) = 0, вероятность того, что a_i=1 равна P(x)=P(0). Например, получается так: a_1=0, a_2=0, a_3=1. 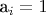В этот момент сумма (*) становится равна 1 и, соответственно, вероятность P того, что a_i=1 становится равной P(1), и так далее.
Требуется найти f(x), учитывая, что x и f(x) стремятся к бесконечности.
Получается так: f(x)=\sum\limits_{i=0}^{x-1}\frac{1}{P(i)}
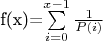
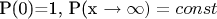
Фурмулу для вероятности не привожу, ибо она мудреная немного. P(0)=1, P({x \to \infty})= const P меняется монотонно.

[--mS--]

Да уж, почти ни единого слова понятного нет. Можно сначала (если, конечно, хотите: может ведь получиться, что объяснять постановку придётся долго, а проку будет пшик) - кто тут бернуллевские независимые случайные величины, каковы вероятности каждой из них равняться единице, кто такие $x(i)$, означает ли $x(i=0)$ просто $x(0)$ и что такое это загадочное $i$, как задаётся функция $P(i)$, кто такое $x$ - число или случайная величина.

[PAV]

[mod="PAV"]Тема перемещена в карантин. Почему это произошло, можно понять, прочитав тему
Что такое карантин и что нужно делать, чтобы там оказаться
Там же описано, как исправлять ситуацию.[/mod]

(GSav, прочитайте в теме инструкцию по правильному оформлению формул и исправьте свои посты)