Определитель какая-то слишком сложная вещь. Подумайте, если обе матрицы не полного ранга, то какие (относительно друга) вектора у них могут быть в ядре, а потом подумайте про проекторы ну и получится пример. Как-то криво я сказал, в общем думайте про проекторы :)
На лекциях которые слушал я тоже пока понятия ядра не было (правда лекции уже и закончились), но определитель, а точнее его свойство мультипликативности играет ключевую роль в понимании и доказательстве задачи:
1. Определитель как функция ранга матрицы порядка

не инъективен — он отображет

рангов в "ноль" и только один ранг в "не ноль".
2. Исходя из п.1 ошибочно полагать две матрицы порядка

с нулевым определителем одинакового ранга.
3. Верно однако полагать имеющими одинаковый ранг две матрицы порядка

с ненулевым определителем
4. По свойству мультипликативности

. Это равенство не утверждает что для произведения в обратном порядке будет тоже значение, но это несложно следует из коммутативности произведения определителей как чисел:
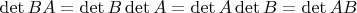
5. Значит значение определителя не зависит от расположения множителей.
6. Из п.3 и п.5 следует ключевое наблюдение: если ненулевой определитель однозначно определяет ранг произведения, и, в том числе ненулевой определитель не меняется при перестановке множителей, то не может быть таких матриц что их произведение в одном порядке невырождено, а в другом вырождено.
7. Значит, если произведение и может давать разный ранг, то только будучи вырожденным, то есть меняться если и может то только ранг
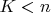
на ранг

.
8. На основании п.7, ограничиваясь рассмотрением матриц порядка

, остаётся рассмотреть ранг

.
Но меняться ему по п.7 не на что кроме как на ранг 0.
9. Приходим к паре матриц вида:
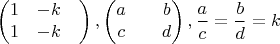
Условие равенства отношений означает линейную зависимость между строками, то есть вырожденность правой матрицы. Произведение матриц указанного вида в одном порядке имеет ранг ноль, а в другую ранг один.