Доброе время суток!
Заранее извиняюсь, если данная тема создана не в том разделе, и прошу модераторов определить ее по назначению.
В данной теме я хотел бы поделиться некоторыми собственными построениями, которые я проделал чтобы посчитать количество симметричных расстановок крестиков да доске для игры в крестики и нолики (мне удалось немного обобщить данную задачу). Возможно, все нижеизложенное уже где-то описано и давно разобрано.
1) Множество зеркальное относительно функции.
Пусть дано множество

и функция

, определенная в том числе и на

. Будем называть множество

зеркальным относительно

, а функцию

отражающей функцией, если выполнены следующие 2 условия:
1) Замкнутость относительно

.
Для всех элементов

множества

элемент

также лежит в

.

2) Сопряженность относительно

.
Для всех элементов

множества

элемент

.

Замечания:
1) Договоримся считать пустое множество зеркальным относительно любой функции для удобства (если необходимо в дальнейшем непустота будет оговариваться).
2) Элемент

будем называть сопряженным с элементом

.
Предложение 1.
Если множества

и

зеркальны относительно функции

, то их объединение также зеркально относительно

.
Доказательство.
Рассмотрим два случая:
1) Множества

и

не имеют общих элементов.
Тогда из определения зеркальных множеств следует:


Очевидно:

Аналогично показываем сопряженность, стало быть сумма двух непересекающихся зеркальных множеств также зеркальна.
2) Множества

и

имеют общие элементы.
Тогда существует непусто множество

Оно, очевидно, зеркально относительно

, исходя из тех же соображений, что и в пункте 1.
Введем еще два множества

, тогда остается показать их зеркальность относительно

, и тогда, так как они не имеют общих элементов, их сумма будет также зеркальна относительно

.
Покажем зеркальность

(Для

доказывается аналогично.
2.1) Для начала покажим выполнение сопряженности относительно

:

Но это верно, так как

, а

зеркально относительно

2.2) Докажем замкнутость относительно

:

Предположим, что это не выполняется, тогда будет существовать элемент

, такой что


Но так как

.
А

зеркально относительно

, тогда

.
Но так как

зеркально относительно

, то то элемент сопряженный с элементом

также должен лежать в

, но мы уже доказали что

. Противоречие, значит

замкнуто относительно

, а значит зеркально относительно

.
Предложение 2.
Всякое зеркальное относительно

множество

(в дальнейшем фразу зеркально относительно

буду опускать) можно представить как сумму двух зеркальных множеств, причем если мощность

больше 2, то двух непустых зеркальных множеств.
Доказательство.
Выберем из

произвольное число несопряженных друг с другом элементов, а потом добавим к ним сопряженных с ними, получим множество

. Оно очевидно зеркально, так как сопряженность следует из сопряженности

, а замакнутость из построения.
Остается показать зеракальность множества

1) Множество P сопряжено, что следует из сопряженности

.

2) Докажем замкнутость

.
Предположим, что это не так, тогда существует

такой, что

, но так как

, то

, а значит

, но так как

зеркально, то тогда

, что неверно, так как мы уже доказали, что

. Противоречие, значит

замнкуто и сопряжено, а значит зеркально.
Вот мы и разбили множество

на два зеркальных множества. Если мощность

больше 2, то в

достаточно положить 1 элемент и сопряженный к нему. Тогда в

останется хотябы 1 элемент.
Задача 1.
Дано конечное непустое множество

мощностью

. Сколько существует функций вида

, относительно которых

зеркально?
1) Для начала вычислим количество функций, относительно которых множество

не зеркально. Поскольку

конечно, то функции могут быть полностью заданы таблицей:




Так как для зеркальности требуется сопряженность, то мы свободно можем определить только половину таблицы, число отражающих функций

(где

- деление нацело с округлением вниз, вроде бы правильно)
-- 18.10.2015, 14:12 --Задачи, которые я еще пока не решил:
Задача 2.
Дано непустое, конечное множество

мощностью

. Сколько существует функций вида

, относительно которых не зеркально ни одно непустое подмножество

.
Задача 3 (О симметрчных расстановках крестиков на доске).
Назовем областью тривиальности функции такое множество агрументов

, что

.
Дано непустое, конечное множество

и функция

, и известная ее область тривиальности

.
Сколько существует зеркальных относителньо

подмножеств

?
Набросок решения:
По предложению 2 каждое зеркальное подмножество мощности

можно представить как сумму двух подмножеств мощности

и
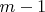
, так мы сможем снижать мощность рассматриваемых подмножеств, а количество зеркальных подмножеств мощности 1 и 2 нам известны из области тривиальности.
Часть 2. Определение симметричного множества относительно f.
Часто когда речь идет о симметрии геометрической подразумевается равенство "расстояний от точки и ее отражения до центра симметрии", но как нам адптировать это представление в нашу модель? Я пока рассматривую такой вариант (для полностью упорядоченных множеств)
Множество

симметрично относительно функции

, если оно зеркально отностлньо

и выполнено условие:

То есть для всех элементов

отражение любого элемента

большего

, будет меньше чем отражение

. Из этого следует, что например множество натуральных чисел не симметрично относительно никакой функции.