ассоциативность умножения матриц

[Oleg Zubelevich]

epros в сообщении #1050939 писал(а):

доказывать ассоциативность матричного произведения из ассоциативности композиций линейных отображений, не определив каким-либо образом связь одного с другим

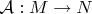
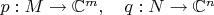
Так вопрос ни кто не ставил. Сначала дается инвариантное определение линейного оператора $\mathcal A:M\to N$. Потом в пространствах $M$ и $N$ вводятся базисы и устанавливается изоморфизм $p:M\to\mathbb{C}^m,\quad q:N\to\mathbb{C}^n$. Птом восстанавливается матрица $A$ оператора $\mathcal A$; матрица определена однозначно в силу единственности разложения по базису. 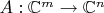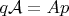Путем умножения этой матрицы на вектор-столбец получаем оператор $A:\mathbb{C}^m\to \mathbb{C}^n$ -- тут как раз и вводится умножение матрицы на вектор-столбец, и убеждаемся, что $q\mathcal A=Ap$ -- коммутативность диаграммы соответствующей. 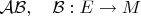А дальше строится матрица оператора $\mathcal A\mathcal B,\quad \mathcal B:E\to M$ И просто по построению оказывается, что это $AB$. Само определение произведения матриц на этом этапе и вводится. И автоматом отсюда получается ассоциативность.
Это просто если изучать эти вещи как они есть, а не по кускам и не из высоких педагогических соображений.

[epros]

Oleg Zubelevich, если Вы предлагаете студенту, которому дали задачу доказать ассоциативность матричного произведения, предварительно ознакомиться со всей этой общей математикой, то по-моему это даже на довольно низкие педагогические соображения не тянет.

А вот если бы Вы предложили студенту вместо копаний в порядке суммирования воспользоваться тем, что произведение матрицы на столбец является столбцом, то может быть из этого и получилось бы упрощение задачи.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);

leolev, уберите картинку из стартового поста, пожалуйста, и наберите формулы.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.