В общем то проблема заключается в том, что не могу найти информацию по этой теме. Для действительных чисел теорию нашел.
То, что мне надо это:
"Два комплексных числа

,

эквивалентны если

такие, что

и

.
Хотелось бы узнать методы приведения комплексных чисел. Кажется, каждое комплексное число эквивалентно (в моем смысле) одному и только одному комплексному числу из множества: Часть верхней полуплоскости от
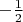
до

и с вырезанным в ней кругом радиуса 1.