Конечные алгебры над F2

[kp9r4d]

Есть ли какая-нибудь классификация конечных алгебр над $\mathbb{F}_2$? А если они достаточно регулярные (коммутативные, ассоциативные, с единицей, central simple)?
Например такой вопрос: любая ли конечная алгебра над $\mathbb{F}_2$ сюръективно вкладывается в алгебру матриц над $\mathbb{F}_2$ достаточно большого размера? Что можно было бы почитать о таких вопросах? Теория представлений - она о том, или не?

[patzer2097]

kp9r4d в сообщении #992671 писал(а):

Есть ли какая-нибудь классификация конечных алгебр над $\mathbb{F}_2$?

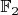
Это просто конечные кольца, в которых выполнено $1+1=0$. Про них многое известно, например, если там нет делителей нуля, то это поля (это касается любой характеристики), если оно просто, то совпадает с матрицами какого-то размера и т. д.

kp9r4d в сообщении #992671 писал(а):

Что можно было бы почитать о таких вопросах?

По теории колец есть масса литературы, в советское время появилось огромное множество книг и переводов книг по этой теме. Например, книга И.Ламбек, Кольца и модули, была бы отличным стартом. Если же Вас интересуют какие-то другие специальные вопросы именно про конечные кольца, то лучше всего будет начать отсюда и выбирать ссылки, которые Вам лучше подходят.

[kp9r4d]

Спасибо!

[kp9r4d]

Я не пойму такой момент. В вики, как я понял, написано, что любое конечное простое кольцо изоморфно кольцу матриц над конечным полем.

Цитата:

More specifically, any finite simple ring is isomorphic to the ring M_n(\mathbb{F}_q) of n by n matrices over a finite field of order q.

Но ведь легко построить простое кольцо из четырёх элементов, например $0,1,i,1+i$ где $i^2 = 1, 1+1=i+i=0$ которое простое, но, очевидно, не существует кольца матриц из четырёх элементов ($Mat_{n \times n} (F_q)$ содержит $q^{n^2}$ элементов), каким образом разрешается это "противоречие"?

[patzer2097]

в Вашем кольце $\{0,1+i\}$ - это идеал

[kp9r4d]

Точно, спасибо.

[kp9r4d]

Вопрос такой: а есть ли какая-нибудь база данных конечных колец? Я загуглить не смог, в Mathematica вроде вообще нет дефолтных инструментов для работы с кольцами (только с группами). В вики есть ссылка где кто-то вручную выписал все кольца порядка $4$, хотелось бы такое для любых порядков (ну или хотя бы не очень больших). Если кто знает что-то подобное, буду благодарен.