(Прошу не спешить с оргвыводами, потому что я, действительно, хочу разобраться, как сделать так, что бы всё было корректно и возможно ли это сделать; спасибо за помощь). Итак, формулировка задачи:
Пусть есть уравнение

Требуется выяснить существуют ли при целых ненулевых

решения

c тремя целыми ненулевыми действительными частями.
Не ограничивая общности, будем рассматривать только ненулевые натуральные

. Тогда известно минимальное относительно переменной

решение

. Допустим, что в заданной области определения существует решение, отличное от минимального. Решение, следующее за минимальным обозначим

.
Подставим в исходное уравнение существующее, по предположению, значение

и будем искать соответствующие ему

, решая кубическое уравнение. Т.к.

, то

, где

натуральное ненулевое. Подставив в исходное уравнение, получим:

Это уравнение имеет один положительный и два комплексных корня с отрицательной действительной частью. В этом уравнении сделаем замену переменных, подставив вместо
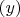


,где

действительная часть комплексного корня. Получим уравнение:

Это уравнение уже имеет симметричные мнимые комлексные корни, т.к.

. Следовательно по теореме Орландо это возможно только при

в уравнении

. Т.е. должно выполняться условие:

Это условие не выполняется, если

. У нас по теореме Виета

. Тогда

. Учитывая область определения, получаем, что

. Практическая подстановка в исходное уравнение показывает, что

, тогда

. И левая часть не равна нулю. А, по предположению о существовании решения отличного от минимального, должна равняться нулю. Противоречие. Значит, решения, отличного от минимального, не существует.
Deggial, теперь все Ваши контрпримеры и довыды находятся вне области определения и рассмотрения. Нужны другие.



