Решенеи ДУ с разделяющимися переменными: модули

[Anna from Svetl]

Рассмотрим ДУ:

$$ \dfrac{dy}{dx} = \dfrac{1}{2}y(x)(y^2(x)-1)\,\dfrac{\dfrac{dV(x)}{dx}}{V(x)}. $$

Разделяем переменные:

$$ \dfrac{2dy}{y(y^2-1)} = \dfrac{d(V)}{V}. $$

Интегрируем:

$$ \ln\left|\dfrac{y^2-1}{y^2}\right| = \ln\left|CV\right|. $$

Мне нужно получить $y^2$ как функцию от $x$ в явном виде. Вопрос, что дальше делать с этими логарифмами и модулями? Как снять их корректно?
Сначала я рассуждала так. Снимем знак логарифма:

$$ \left|\dfrac{y^2-1}{y^2}\right| = \left|CV\right|. $$

Пусть $y^2>1$. Тогда

$$ y^2=\dfrac{1}{1-|CV|}. $$

Теперь пусть $y^2<1$. Тогда

$$ y^2 =\dfrac{1}{1+|CV|}. $$

Оба выражения являются решением исходного уравнения.
Но ведь функции

$$ y^2=\dfrac{1}{1-CV}\quad\text{и}\quad y^2=\dfrac{1}{1+CV} $$

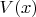
также являются решением исходного уравнения, что легко проверить подстановкой. Но ведь если $V(x)$ меняет знак при некотором $x$ эти два решения ведут себя иначе, чем решения, приведенные выше.
Никак не могу понять, как же все-таки правильно записать общее решение для этого ДУ.

[provincialka]

Anna from Svetl в сообщении #992655 писал(а):

функции

$$ y^2=\dfrac{1}{1-CV}\quad\text{и}\quad y^2=\dfrac{1}{1+CV}$$

Ничем не отличаются друг от друга, кроме обозначения константы.

[Anna from Svetl]

Да бог с ней, с константой. Меня интересует отличие этого решения от того решения, где $V$ находится под знаком модуля.

[ex-math]

Разберитесь для начала с уравнением попроще: $y'=y/x$. Как здесь снять модуль понятно?

[Anna from Svetl]

В этом уравнении просто снимают модули с обеих сторон уравнения во всех решениях, которые я видела. Хотя почему, например, нельзя записать

$$ y=C|x|, $$

мне непонятно.

[ex-math]

Потому что обычно хотят видеть в качестве решения дифференцируемую функцию.
Почему Вас смущают аналогичные действия для Вашего уравнения?

[Anna from Svetl]

Даже если в качестве решения хотят видеть дифференцируемую функцию, это же не отменяет того, что $y=C|x|$ --- решение уравнения? Вы ведь не будете отрицать, что и и решение с модулем, и решение без модуля являются решениями данного уравнения. Но ведь общее решение должно быть одно, разве нет? И ведут себя эти решения по разному.

[ex-math]

Ну как, при $x=0$ возникают проблемы с подстановкой $y=C|x|$ в уравнение. Если $x=0$ выбросить, то получится две области, и решения в этих областях не обязаны как-то коррелировать в плане знака и величины $C$. Тогда и $y=2x$ при $x>0$, $y=-x$ при $x<0$ -- решение.

[Anna from Svetl]

А исходя из чего тогда делать выбор: с модулем иди без модуля решения?

[ex-math]

Если Вы не в окрестности нуля, то модуль не нужен, все варианты знаков вбирает в себя константа.
А если в окрестности нуля, то из дифференцируемых функций будет только решение без модуля.
Так что в Вашей задаче я бы убрал модули как только они появились, с оговоркой о знаке $C$.

[Anna from Svetl]

Спасибо за помощь.

[svv]

Anna from Svetl в сообщении #992655 писал(а):

$$\dfrac{2dy}{y(y^2-1)} = \dfrac{d(V)}{V}$$

Это уравнение можно без логарифмов и модулей привести к виду
$d\left(\dfrac{y^2-1}{y^2V}\right)=0$