Как измерить статистическую значимость?

[Anton_Peplov]

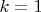
Я вписал в экспериментальный ряд $\{(x_i, y_i)\}$ зависимость $y = bx^k$ методом максимального правдоподобия. Теория явления предсказывает, что $k = 1.5$. У меня получилось, что $k = 1$. Теперь мне надо понять, значим ли полученный результат или представляет собой статистическую погрешность. Но я не знаю, как измеряется статистическая значимость.

В качестве пробы я сделал вот что. Обозначим коэффициенты $k$ и $b$, определенные экспериментально, как $k^E$ и $b^E$. Коэффициент $k$, предсказываемый теорией, обозначим $k^T$. Коэффициента $b$ теория не предсказывает, но метод максимального правдоподобия дает формулу $b = b(k, \{(x_i, y_i)\})$, по которой я вычислял $k$ и $b$. Подставив в нее $k^T$, получим некоторое значение $b$ - значение при теоретическом $k$ и данном экспериментальном ряде. Обозначим его $b^T$.

Построим кривую по данному ряду $\{x_i\}$ кривые $y^E = b^Ex^{k^E}$ и $y^T = b^Tx^{k^T}$. Подсчитаем суммы квадратов отклонений фактических значений $\{y_i\}$ от предсказываемых этими кривыми:

$$ S^E = \sum\limits_{i = 1}^{n}(y_i - y^E_i)^2 $$

$$ S^T = \sum\limits_{i = 1}^{n}(y_i - y^T_i)^2 $$

У меня получилось, что $S^E$ меньше $S^T$ в два с половиной раза. Но я не знаю, достаточно ли этого, чтобы утверждать, что на самом деле имеет место коэффициент $k^E$, а не $k^T$. Это самопальный метод, который я только что придумал на коленке. Должны быть стандартные. Подскажите, какие есть?

Да, если есть трудности с методом максимального правдоподобия, можно перейти к логарифмическим координатам и посчитать методом наименьших квадратов. При нормальном законе распределения $Y$ закон распределения $\ln Y$ тоже почти нормален, поэтому МНК работает хорошо. Во всяком случае, дает точно такое же значение $k^E$, я проверил.

[Евгений Машеров]

Лично я бы работал с логарифмированной моделью. Тут, разумеется, надо понять спецификацию ошибки, если она мультипликативная $y=bx^ke^{\varepsilon}$
$\varepsilon\sim N(0,\sigma^2)$
то логарифмирование не просто упрощающий вычислительный приём, а приведение к нормальному распределению ошибок, а если аддитивная
$y=bx^k+\varepsilon$
то логарифмирование искажает распределение, и может быть оправдано, как приём упрощения, лишь при малом $\varepsilon$
Различить эти ситуации можно, скажем, построив график зависимости невязки модели (или же её квадрата или абсолютной величины) от y, если спецификация правильна, зависимость не просматривается.
Чаще бывает мультипликативная спецификация.
После логарифмирования модель линейна (линеаризована) и для неё можно рассчитать по известным формулам стандартные ошибки коэффициентов. Далее считается t-отношение, только сравнивает не с нулём, а с теоретическим значением.
Для аддитивной спецификации считал бы через F-отношение.

[Anton_Peplov]

Евгений Машеров в сообщении #991673 писал(а):

После логарифмирования модель линейна (линеаризована) и для неё можно рассчитать по известным формулам стандартные ошибки коэффициентов. Далее считается t-отношение, только сравнивает не с нулём, а с теоретическим значением.
Для аддитивной спецификации считал бы через F-отношение.

Ввел в Google запросы "t-отношение" и "F-отношение". Ничего последовательного и внятного не обнаружил. Не могли бы Вы назвать учебник, в котором о них можно прочесть? И заодно уж об "известных формулах для стандартных ошибок коэффициентов"?

[Евгений Машеров]

Ну, вообще-то в любом учебнике матстатистики, начиная с элементарного уровня. Я даже затрудняюсь рекомендовать конкретный, если Вы назовёте, какой у Вас под рукой, я скажу, в какой главе. Ещё можете искать на "критерий Стьюдента" и "F-критерий Фишера". И выражения для дисперсий оценок коэффициентов парной регрессии там же.