В книге "Теория чисел" в виде задачи дан алгоритм нахождения приведенного модуля, подобного данному, в мнимом квадратичном поле(зад.24, стр.173):
Пусть

из квадратичного мнимого квадратичного поля удовлетворяет условиям

, но не является приведенным (то есть, модуль

меньше 0). Положим

, где
целое рациональное

выбрано так, что

. Если
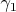
не приведенное, то аналогично полагаем

и т.д. Требуется показать, что за конечное число шагов мы получим приведенное число.
Пытаюсь решить так: предположим модуль каждого числа

из последовательности будет меньше 1, тогда последовательность мнимых частей этих чисел возрастает и имеет предел. Если этот предел не равен

, то противоречие получается легко. Помогите, пожалуйста, со случаем, когда предел равен

. Или, может, есть какой-то другой путь решения. Задача, по-моему, непосредственного отношения к теории чисел не имеет...