Задача по планиметрии

[TOTAL]

Через центр описанной окружности провели диаметр $AD.$
Через т. $F$ (середину $CB$) провели $PD=2DF.$
Получили точку $P$ - точку пересечения высот тр-ка $ABC.$
(По построению, $P$ - это центр описанной окружности вокруг тр-ка, для которого тр-к $ABC$ является срединным.)
Синие линии перпендикулярны (по условию).

Очевидно, $AQ$ является высотой и биссектрисой в тр-ке $PAO,$
поэтому $AP=AO=2OF,$ поэтому угол $COB=120$ ($OF$ равно половине радиуса)

[Skeptic]

Что такое срединный треугольник?
Если точка $P$ - центр описанной окружности, то почему она не лежит на диаметре $AD$?

[AVV]

TOTAL в сообщении #977169 писал(а):

$PD=2DF.$

Ммм, а как это увидеть? Тогда и то, что $CB$ пополам делит $OE$, наверное, станет понятно.

(Оффтоп)

Кстати, в какой программе вы рисовали?

[TOTAL]

AVV в сообщении #977465 писал(а):

TOTAL в сообщении #977169 писал(а):

$PD=2DF.$

Ммм, а как это увидеть?

Что увидеть? Я провел $PD$ так, что $PD=2DF$. Не верите, что это можно сделать?

-- Пт фев 13, 2015 08:25:59 --

Skeptic в сообщении #977302 писал(а):

Что такое срединный треугольник?

Это треугольник, вершинами которого являются основания медиан.

[AVV]

TOTAL в сообщении #977558 писал(а):

Что увидеть?

Что это точка пересечения высот.

[TOTAL]

AVV в сообщении #977733 писал(а):

TOTAL в сообщении #977558 писал(а):

Что увидеть?

Что это точка пересечения высот.

Там есть подсказка про то, что это центр окружности, описанной вокруг треугольника, для которого исходный треугольник является срединным. Точка $D$ - центр окружности, описанной вокруг треугольника, который в два раза больше исходного.

(Здесь дважды гомотетия: сначала с центром в т.$A$ с коэффициентом $2$, затем с центром в т.$F$ с коэффициентом $-1$.)

[Skeptic]

TOTAL, вы исходите из предположения, что $\angle A=60^{\circle}$, а это надо доказать.
Совершенно не очевидно, что $PQ=QO$.
Не доказано, что точка $F$ - общая точка пересечения прямых $CB$, $PD$ и $OE$.
Не доказано, что точка $F $ делит $OE$ пополам.

[TOTAL]

Skeptic в сообщении #979019 писал(а):

TOTAL, вы исходите из предположения, что $\angle A=60^{\circle}$, а это надо доказать.

Я не исхожу из такого предположения, я это доказал. Откуда Вы взяли, что "исхожу"?

[Skeptic]

TOTAL в сообщении #977169 писал(а):

Очевидно, $AQ$ является высотой и биссектрисой в тр-ке $PAO,$
поэтому $AP=AO=2OF,$ поэтому угол $COB=120$ ($OF$ равно половине радиуса)

Это нужно доказать!

[TOTAL]

Skeptic в сообщении #979127 писал(а):

TOTAL в сообщении #977169 писал(а):

Очевидно, $AQ$ является высотой и биссектрисой в тр-ке $PAO,$
поэтому $AP=AO=2OF,$ поэтому угол $COB=120$ ($OF$ равно половине радиуса)

Это нужно доказать!

Что нужно доказать? Что гипотенуза в два раза длиннее катета, лежащего против угла 30 градусов?

[OlegCh]

TOTAL в сообщении #979445 писал(а):

Что нужно доказать?

Что $AQ$ является биссектрисой в тр-ке $PAO$, разумеется.

[TOTAL]

OlegCh в сообщении #979474 писал(а):

TOTAL в сообщении #979445 писал(а):

Что нужно доказать?

Что $AQ$ является биссектрисой в тр-ке $PAO$, разумеется.

$FO \parallel PA$ Дальше сами (можно смотреть на рисунок)

[OlegCh]

Мой вариант решения.


Здесь зеленые - высоты, синие - медианы, оранжевая - биссектриса угла $A$.
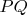
$PQ$ - прямая, которой перпендикулярна наша биссектриса.
Поскольку в тр-ке $APQ$ биссектриса является и высотой, то тр-к $APQ$ равнобедренный и $\angle P=\angle Q$. Докажем, что $\bigtriangleup APQ$ оказывается одновременно и равносторонним.
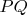
Поскольку $PQ$ по определению является прямой Эйлера, то пересечение с ней серединного перпендикуляра стороны $AC$ дает точку $O$ - центр описанной окружности.
Покажем, что углы $BAH$ и $OAC$ равны.
Пусть луч $AO$ пересекает описанную окружность в точке $B'$, тогда углы $ABC$ и $AB'C$ равны, поскольку опираются на одну и ту же хорду $AC$. Т.к. $AB'$ - диаметр, то в тр-ке $AB'C$ угол $C$ прямой, поэтому в этом тр-ке $\angle A=90^{\circ}-\angle B'$. Аналогично, поскольку $AA_H$ высота, то в тр-ке $ABA_H$ $\angle A=90^{\circ}-\angle B$. Отсюда углы $BAH$ и $OAC$ равны.
Из равенства этих углов и равнобедренности тр-ка $APQ$ следует, что $PH=OQ$, следовательно тр-ки $PC_HH$ и $OB_MQ$ равны по стороне и двум углам (ну то, что углы O и H равны, это понятно?). В этих тр-ках высоты, опущенные на прямую Эйлера, стало быть тоже равны, поэтому $C_HB_M\parallel PQ$. Но $\triangle AC_HC$ прямоугольный и $C_HB_M$ его медиана, поэтому $C_HB_M=AB_M$. А т.к. тр-к $AC_HB_M$ к тому же ещё и равнобедренный, то он равносторонний. Отсюда сразу следует, что $\angle A=60^{\circ}$ и заодно что $\triangle APQ$ равностороний. Уф... (это вместо чтд).

[Skeptic]

Ещё одно решение.
Переместим вершину искомого $\angle A$ по описанной окружности так, чтобы одна сторона треугольника совпала с диаметром описанной окружности. Получим прямоугольный треугольник. Медиана, проведённая с прямого угла сопадает с линией, соединяющей точки пересечения меридан и высот. Треугольник, образованный вершиной $\angle A$ и медианой из прямого угла - равнобедренный относительно биссектрисы $\angle A$, но его боковая сторона и основание (медиана) равны радиусу описанной окружности. Следовательно $\angle A=60^{\circle}$.

[OlegCh]

Skeptic в сообщении #979576 писал(а):

Переместим вершину искомого $\angle A$ по описанной окружности так, чтобы одна сторона треугольника совпала с диаметром описанной окружности.

Ну так это же будет другой треугольник...