Вот два объяснения появления этого первого интеграла.
1. С Лагранжевой точки зрения.
Рассмотрим механическую систему

, где

- конфигурационное многообразие,

- квадратичная форма кинетической энергии,

- силовая форма не обязательно потенциальная.
Пусть

- гладкое векторное поле на

. Обозначим

(

- внутреннее умножение и

далее производная Ли).
Уравнения движения имеют первый интеграл, квадратичный по импульсам вида

, где

линейная по скоростям форма,

гладкая функция на

который находится квадратурами, тогда и только тогда, когда существует на

гладкое векторное поле

такое, что

и форма

точна. (Что-то вроде обобщения теоремы Нётер для квадратичных интегралов). В нашем случае

.
Условия утверждения выполняются и

.
2. С гамильтоновой точки зрения.
Потенциальная функция

однородна степени

.
На фазовом пр-ве

положим

. Функции

порождают алгебру Ли изоморфную

. Из невырожденной формы Киллинга на ней и отображения момента появляется первый интеграл уравнений движения

.
Т.е.

, где { } - скобка Пуассона. Потенциальную функцию можно усложнить, добавив к ней
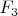
. Оба утверждения справедливы для любой размерности.



