В качестве приложения данной теории предлагается следующая верссия теоремы о множителях Лагранжа для билинейных отображений.
Рассмотрим векторные пространства

. И пусть

билинейная сюръекция; отображение

тоже билинейно.
Утверждение. Предположим, что
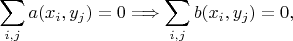 суммирование ведется по конечному набору индексов.
суммирование ведется по конечному набору индексов.
Тогда существует линейное отображение  такое, что
такое, что  .
.Действительно,

, где

-- каноническое отображение, а

-- линейные отображения. Причем по условию

. Теперь утверждение следует из стандартного факта:

.
зы жалко я диаграммки рисовать не умею, здесь это тоже было бы уместно