Существуют числа при делении на которые степеней с основаниями меньшими чем эти числа, получатся разные остатки. Например, для кубов это простые числа:2, 3, 5, 11,17,23,29,41,47,53,59,71,83…Есть предположение, что для чисел больших

это свойство имеют все простые числа вида
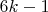
. Тогда этим свойством обладают и произведение двух неравных чисел этого вида. Например:

. Приведем числовой пример. Остатки ряда кубов

для делителя

соответственно имеют значения

, а для делителя

, ряд из 32 кубов для этого делителя, имеет также не повторяющиеся остатки

Далее понятно, что вторая степень

из УФ при целых числах должна удовлетворять условию

, следовательно,

Степень

в системе счисления с основанием равным основанию степени имеет вид

. Где индекс

обозначает основание системы счисления. Тогда любая другая степень

при условии

в этой системе счисления будет иметь одноразрядное основание (одной из цтфр этой системы счисления). Тогда с учетом (1) в системе счисления с основанием

степень

является

-разрядным числом. А сумма двух степеней будет иметь вид
![$$a^p +b^p=10^p_a+[b^p_a]=1[b^p_a],$$ $$a^p +b^p=10^p_a+[b^p_a]=1[b^p_a],$$](https://dxdy-02.korotkov.co.uk/f/9/7/9/979af68e5e8304be93de5d483ca95f0682.png)
где квадратные скобки означают, что внутри скобок находятся значения разрядов указанного числа. То есть
![$$10^p_a+b^p_a =1\makebox{\underbrace{000…0}_{p}}_a + \makebox{\underbrace {[\alpha\beta\gamma...}_{p}]_a} =1 \makebox{\underbrace {[\alpha\beta\gamma...} _{p}}]_a \qquad \eqno(2)$$ $$10^p_a+b^p_a =1\makebox{\underbrace{000…0}_{p}}_a + \makebox{\underbrace {[\alpha\beta\gamma...}_{p}]_a} =1 \makebox{\underbrace {[\alpha\beta\gamma...} _{p}}]_a \qquad \eqno(2)$$](https://dxdy-03.korotkov.co.uk/f/e/5/1/e51bea1ac306f3c2e61ddebd9435028082.png)
Например, для суммы кубов

Как видно, правая часть (2), отличается от

только старшим разрядом равным

.
На основании этого делаем вывод. Если в уравнении Ферма имеется хотя бы одна степень с основанием

, которое являясь делителем ряда

не дает равных остатков, то для таких

ВТФ верна. Докажем сначала для кубов Действительно, правая часть (2) не может быть кубом, так как в этом случае основание этого куба,в связи неповторяемости остатков, равнялось бы сумме оснований

, что невозможно при натуральных значениях

. Дальнейшее рассуждение по данной теме можно продолжить



