provincialkaЕсть. Мне проще будет рекуррентное уравнение степени

записывать в виде

. Введем оператор увеличения индекса, которые действует на последовательность так

,

и т.д. Тогда линейное рекурретное уравнение можно записать в виде

, где

-- многочлен с постоянными коэффициентами. Если теперь

удовлетворяет уравнению

,

удовлетворяет уравнению

, то

будет удовлетворять уравнению

.
Для доказательство надо подставить  и еще учесть, что
и еще учесть, что  , т.к. это многочлены от одного и того же оператора
, т.к. это многочлены от одного и того же оператора  .
.Ну вот, уже все решили )
-- Пн янв 26, 2015 00:23:53 -- Правда, может получиться не минимальный.
Да, вместо
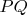
подойдет наименьшее общее кратное

и

.



