AsalexЯ получу ещё деривационные формулы своим способом, добавлю взаимосвязей.
Латинские индексы меняются от

до
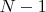
, греческие от

до
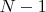
. Тем самым выделяется координата

.
Координаты обозначаю

, смысл

тот же, что у Ваших

, а

, наверное, аналогична Вашей

.
Индекс после запятой — производная по соответствующей координате.
Начинаю с формул

и

. Их обоснование — отдельный разговор. Векторы

— это просто векторы координатного базиса в соответствующей точке.
Фиксируя

, получаем поверхность, скажем,

. Требуем, чтобы на этой поверхности было

и

. Это значит, что

— единичная нормаль к поверхности.
Имеем

Полагая отдельно

и

, получим


Это и есть деривационные формулы. Но не все связи установлены. Учтем, что

константа при любом

:


Полагая

, получим

. Это ответ на Ваш вопрос о взаимосвязи тензоров

и

.
Полагая

, получим

, и второе слагаемое из формулы для

вычеркивается.
Но сказать, что система

(Ваша

) здесь совсем никак не маячит, нельзя. Именно она задаёт смысл понятию параллельного переноса вектора из одной точки в другую, необходимому для дифференцирования векторов

по координате.