Спектр сигнала

[grelik]

Задан следующий прямоугольный сигнал:
Подскажите пожалуйста как мне найти спектр этого сигнала в ручную, какие формулы использовать?
Предполагаю что нужно использовать эту формулу: $f(t)= \frac {4V} {\pi} \sum\limits_{k=1}^n \frac {\sin k\omega t} {k} $ , но как то не получается, не понятно что туда подставлять...
Допустим подставлю на место амплитуду 9 $V$ , $\omega= \frac {2\pi}{T} $, $T= 0.025 $ сек (т.к частота 40гц),
при $ k=1: {(\frac {36}{3.14})} {(\frac {\sin 1 \cdot 251,32 \cdot 1 }{1})} =49 $
Вообщем подскажите та ли формула и как ей пользоваться, чтобы результат аналитических вычислений спектра примерно совпал с результатом моделирования:

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
1. Запишите формулы в соответствии с требованиями Правил форума, т.е. в $\TeX$.
Краткие инструкции можно найти здесь: topic8355.html и topic183.html.
Кроме этого, в теме Видео-пособия для начинающих форумчан можно посмотреть видео-ролик "Как записывать формулы".

2. Приведите свои попытки решения и/или укажите затруднения.

После того, как исправите сообщение, сообщите об этом в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (Ф)»
Причина переноса: не указана.

[profrotter]

Первым делом следует закрыть программу по моделированию, взять ручку- карандаш-проч., много листов бумаги. Изобразить временную диаграмму сигнала и выписать его заданные параметры, после чего можно будет сказать, что задан сигнал. Разложить его в ряд Фурье в тригонометрической форме, вспомнить/посмотреть в учебнике/в лекциях, что называется спектром сигнала, амплитудным спектром, фазовым спектром. Определиться с тем, какой из спектров Вы ищете и будете сравнивать с "результатом моделирования". Найти этот спектр, построить спектральную диаграмму. Сравнить с "результатом моделирования".

Учебники
1. О.А. Стеценко Радиотехнические цепи и сигналы (этот самый простой)
2. Гоноровский Радиотехнические цепи и сигналы
3. Баскаков Радиотехнические цепи и сигналы

[HallBoyCHS]

Необходимо разложить функцию в ряд Фурье: $\frac{a_0}{2}+\sum\limits_{n=1}^{\infty}a_n\cos(n\omega_0t)+b_k\sin(n\omega_0t)$
найти коэффициенты: $a_n=2/T \int\limits_{-T/2}^{T/2}x(t)\cos(n\omega_0t)dt$, $b_n=2/T \int\limits_{-T/2}^{T/2}x(t)\sin(n\omega_0t)dt$, $a_0=2/T \int\limits_{-T/2}^{T/2}x(t)dt$
так как функция не четная, то : $a_n=0$
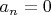
Находишь: $b_n$ и $a_0$
Затем их модули-амплитуды гармоник, $a_0$-амплитуда на нулевой частоте
Строишь график с осями ординат-амплитуда и абсцисс-частота
Откладываешь соответствующие гармоники(члены ряда) на графике, частоты берешь кратные основной частоте исходного сигнала ( частота для первой гармоники равна частоте исходного сигнала) у тебя будут 1, 3, 5,.. гармоники.
Это амплитудный спектр сигнала.