Полная линейная группа

[Braga]

В учебнике разобран пример полной линейной группы. Говорится:
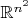
рассмотрим отображение $ det: GL_n (\mathbb{R}) \subset \mathbb{R}^{n^2} \rightarrow \mathbb(R)$ - оно непрерывно(почему?) и отображается на множество $\mathbb{R} \textbackslash \lbrace 0 \rbrace$. Так как $\lbrace 0 \rbrace$ - закрытое множество, то полная линейная группа отображается в открытое множество и следовательно $GL_n (\mathbb{R})$ открытое множество в $\mathbb{R}^{n^2}$. Из чего это следует? Мы отображаем из большей размерности в меньшую, разве можно судить в этом случае об открытости множества?

-- 09.12.2014, 23:43 --

С непрерывностью, впрочем, понятно. При изменениях одного из элементов матрицы изменения будут тоже непрерывными, поскольку функция det - полиномиальная. Но почему прообраз - открытое множество - непонятно

[Otta]

Потому что прообраз всякого открытого множества открыт при (глобально) непрерывном отображении.

[Braga]

Где можно доказательство этого утверждения прочесть? Самому доказать не вышло

[demolishka]

Это определение непрерывности для отображения топологических пространств. В случае метрического пространства оно совпадает с определением непрерывности по метрике. В метрическом пространстве всякое открытое множество представляется в виде объединения открытых шаров. Вам нужно показать, что $U=f^{-1}(V)$ - открыто для всякого открытого $V$. С учетом предыдущего замечания, нужно показать, что каждая точка из множества $U$ входит в это множество с некоторой окрестностью. Ну так это и есть определение непрерывности по метрике на множестве $U$.