Здравствуйте!
Есть такое задание:
Разложить функцию

в окрестности изолированной особой точки и определить характер этой особой точки.
Используем разложение

Получаем:

и

Область сходимости полученного ряда -- кольцо

Полученное разложение, сходящееся в проколотой окрестности точки
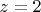
, содержит бесконечное количество слагаемых с отрицательными степенями

, поэтому точка
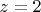
является существенно особо точкой.
Подскажите, пожалуйста, верно ли это? Особенно интересен вопрос правильности перехода от разложения

к разложению

...
Спасибо!



