Что такое вспышка?

[rustot]

ну одинаковая же у вас скорость получилась? этого достаточно. а майкельсон проверял экспериментом совсем другую теорию, в которой скорость разная. в той теории не было никаких сфер и фотонов. в той теории был свет в виде лодочек плывущих по реке-эфиру, медленно против течения и быстро по течению. вот ее то и проверяли этим экспериментом.

[romanov59]

В этой теме я не говорил про опыт Майкельсона. Я говорю про совпадение и нет начал отсчета движущейся ( условно) и покоящейся ( условно) систем отсчета. И пытаюсь показать что по законам классической физики После расхождения точек отсчета каждая как бы остается в центре. Центр один, а другая точка псевдо центр. Тоже центр но как бы.

[rustot]

по законам классической физики если в момент времени 0 начала координат двух систем отсчета, двигающихся друг относительно друга со скоростью $v$ совпадали, то в момент времени $t$ они находятся на расстоянии $v t$ друг от друга. что тут мусолить? вы начала координат называете "центрами" или что то другое? что "остается" в этих центрах я не понял. начала координат остаются в начале координат?

[romanov59]

В момент времени $ t $ расстояние от точки 2 ( на оси $ X $ не в центре) До точки сферы на той же оси $ r -{vt} $ Скорость в этом направлении $ c-v $. Дальше расчет сумеете сделать, а то он ( расчет уже сделан в предыдущих постах) Точка движется за сигналом убирая часть скорости и т. д.

[rustot]

расстояние от точки до начала координат системы отсчета определяется ее координатами в этой системе. $\sqrt{x^2 + y^2 + z^2}$. если она на оси $x$, то значит $y=z=0$ и расстояние равно $x$. при чем тут какие то $r$, $v$ и $t$? могу только попытаться угадать что речь о точке, движущейся в этой системе отсчета по оси $x$ с постоянной скоростью $x = x_0 + v t, y = 0, z = 0$. тогда текущее расстояние до начала координат и равно $x_0 + v t$. что такое $r$ все равно непонятно. так обозначено $x_0$? и что такое $c$?

у вас по всей видимость есть какая то точка, движение которой относительно системы отсчета вы желаете описать. ну так и сделайте это $x = f_1(t), y = f_2(t), z = f_3(t)$, тогда все будет понятно

[romanov59]

Рассмотрим движение строго по оси $ x $ В момент $ t $ из центра т.1 расстояние $ r $ скорость $ c $. Из т. 2 ( не центр) расстояние в одну сторону $ r - {vt} $ скорость $ c-v $, в другую расстояние $ r + { vt} $ скорость $ c+v $. Представьте большее расстояние с большей скоростью за то же время что и меньшее расстояние с меньшей скоростью и среднее со средней и $ t $ есть $ t $ .

[rustot]

вы поймите, кроме вас никто не может понять что вы пишете. вы можете как то по человечески писать?

"В момент $ t $ из центра т.1 расстояние $ r $ скорость $ c $." Вот как это понять? С одной стороны "из центра" (по человечески - из начала координат) должно бы было означать $x(t = 0) = 0$, с другой тут же упоминается какое то расстояние $r$. его куда приткнуть? вы можете написать нормальную формулу $x = ...$, в которую я подставив допустим $t=5$ получу однозначное значение $x$ точки в этот момент времени? допустим $x = c t$. или $x = x_0 - c t$ или $x = - x_0 + c t$

[romanov59]

Вы понять не можете одномерный случай? Две точки совпадали $ t=0 $ Затем разошлись в месте совпадения одна, другая не в центре. От этой другой До мгновенного снимка достижения точек сферы ( еще 2 точки на равном расстоянии от первой) В одну сторону расстояние меньше и скорость меньше в другую расстояние больше и скорость больше. И т. д. Как еще объяснить?

[12d3]

romanov59 в сообщении #935962 писал(а):

Вы понять не можете одномерный случай? Две точки совпадали $ t=0 $ Затем разошлись в месте совпадения одна, другая не в центре. От этой другой До мгновенного снимка достижения точек сферы ( еще 2 точки на равном расстоянии от первой) В одну сторону расстояние меньше и скорость меньше в другую расстояние больше и скорость больше. И т. д. Как еще объяснить?

Я немного понял картину. Есть две точки, одна движется, другая покоится. В момент их совпадения (в начале координат), испускается световой сигнал во все стороны. Потом измеряется расстояния от движущейся точки до фотонов, которые улетели вперед и до тех, которые улетели назад. Так? Только совершенно непонятно, о чем фраза скорость меньше. Скорость чего?

[rustot]

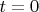
вот честно, не могу понять. вы сами перечитайте что вы написали. реально полагаете что это можно понять "Две точки совпадали $ t=0 $ Затем разошлись в месте совпадения одна, другая не в центре."?

вы можете написать это в виде уравнения движения? все что я понял, вы пишете про две точки. значит будут два уравнения для двух точек $x_1 = ...$, $x_2 = ...$ как функции от $t$. вы можете их записать? тогда можно будет что-то осмысленное говорить уже о скоростях, как о производных от этих уравнений. а сейчас у вас непонятная каша с какими то скоростями непонятно чего относительно непонятно чего.

если же вы запишете $x_1 = f_1(t)$ и $x_2 = f_2(t)$. тогда можно будет и скорость первой точки определить $v_1 = \frac{d}{dt} f_1(t)$ и скорость второй $v_2 = \frac{d}{dt} f_2(t)$ без каких либо недопониманий и двусмысленностей

[provincialka]

romanov59 в сообщении #935962 писал(а):

От этой другой До мгновенного снимка достижения точек сферы ( еще 2 точки на равном расстоянии от первой)

Набор слов
Какой снимок? Что за достижения у точек сферы? Может, для вас русский не родной?
Попытайтесь говорить более короткими предложениями, что ли.

[romanov59]

Нарисуйте ось в центре точка1 на равном расстоянии точки А и В, на оси между т 1 и т А поставьте точку 2. Т 2 движется к т. А расстояние меньше от т 2 до т А скорость тоже меньше света до т 2 Точка2 движется следом за фотоном убирая скорость. Классика! В другую сторону фотон движется от т.2 расстояние увеличивается скорость тоже. В результате $ t $ есть $ t $.

[rustot]

Цитата:

Нарисуйте ось в центре точка1

$x_1 = 0$

romanov59 в сообщении #935980 писал(а):

на равном расстоянии точки А и В

$x_a = 7$
$x_b = -7$

romanov59 в сообщении #935980 писал(а):

на оси между т 1 и т А поставьте точку 2

$x_2 = 6$

romanov59 в сообщении #935980 писал(а):

Т 2 движется к т. А

$x_2 = 6 + v t$

romanov59 в сообщении #935980 писал(а):

расстояние меньше от т 2 до т А скорость тоже меньше света до т 2 Точка2 движется следом за фотоном убирая скорость. Классика!

вот это я уже не осилил. вы можете это тоже перевести на нормальный язык как я сделал выше?

[romanov59]

$ t_1=\frac r c $ Где $ r $ расстояние от т.1 до точек А и В.
$ t_2=\frac {r-{vt}}{ c-v} $ Где $ r-vt $ расстояние от т. 2 до т.А $ c-v $ Скорость между точками 2 и А.
Вычисления что $ t_1 $ и $ t _2 $ Равны приведены в предыдущих постах.

[_Z_]

(Оффтоп)

Классический случай "казнить нельзя помиловать".