Несобственный интеграл через вычеты

[Edmonton]

Добрый день!

Есть такое задание: используя теорему Коши о вычетах, вычислить несобственный интеграл: $\int\limits_0^{\infty} \frac{\ln x}{x^2-1} dx$. При вычислении я получаю ответ, который отличается от правильного на знак. Не могу найти ошибку, помогите, пожалуйста.

При его вычислении я использую стандартный метод решения:
1) Перехожу в комплексную плоскость и рассматриваю в ней область $G(r,R)=B_R(0)\backslash\{\overline{B_r(0)}\cup [r;R]\}$ для каких-то $R>1>r$.
Успешно доказываю, что в этой области есть регулярные ветви многозначной функции $\{ \operatorname{Ln}z\}$
2) Выделяю в $G(r,R)$ регулярную ветвь $h(z)$ многозначной функции $\{ \operatorname{Ln}z\}$ такую, что при $x\in (r;R),y \to +0 $ функция $h(z)=h(x+i \cdot 0)=\ln x$ (т.е. выбрана ветвь на "верхнем берегу разреза"); тогда при $x\in (r;R),y \to -0 $ функция $h(z)=h(x-i \cdot 0)=\ln x + 2 \pi i$
3) Беру в качестве подынтегральной функции $f(z)=\frac{h^2(z)}{z^2-1}$ Рассматриваю интеграл $\int\limits_{\partial G} f(z)dz = \int\limits_{r}^R f(z)dz +\int\limits_{B_R^+ (0)} f(z) dz + \int\limits_R^r f(z)dz +\int\limits_{B_r^- (0) }f(z)dz $

Успешно доказываю, что при $R \to + \infty,\; r \to +0$ это выражение имеет вид: $\int\limits_{\partial G} f(z)dz = - 4 \pi i \int\limits_0 ^{+\infty} \frac{\ln z}{z^2-1} dz +4 \pi ^2 \int\limits_0 ^{+\infty} \frac{dz}{z^2-1}$
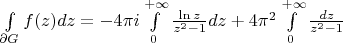
Т.к. в области есть только одна особая точка $-1$, то по теореме Коши о вычетах имеем: $\int\limits_{\partial G} f(z)dz = 2 \pi i \cdot \operatorname{res}_{-1} f(z)$. Считаю вычет в точке $-1:$ т.к. это - полюс первого порядка, то $\operatorname{res}_{-1} f(z) = \frac{h^2(-1)}{-2}=\frac{(\ln 1 +\pi i)^2}{-2}=\frac{\pi ^2}{2} $. Исходя из вышесказанного, имеем следующее: $- 4 \pi i \int\limits_0 ^{+\infty} \frac{\ln z}{z^2-1} dz +4 \pi ^2 \int\limits_0 ^{+\infty} \frac{dz}{z^2-1} = 2 \pi i \cdot \frac{\pi ^2}{2} .$ Оба интеграла, стоящие в левой части - числа действительные, только нужный нам имеет комплексный множитель перед интегралом, а побочный - нет. В связи с этим нам нужна мнимая часть выражения, стоящая справа, которая и будет ответом, а именно: $I=- \frac{\pi^2}{4}$

Помогите, пожалуйста, определить ошибку!

[ex-math]

Вам надо учесть, что точка $1-i0$ -- особая, и обойти ее по маленькой полуокружности. Разве Вы не заметили, что не все из использованных Вами интегралов сходятся?

-- 25.11.2014, 11:54 --

Я бы еще посоветовал рассмотреть в качестве области полукруг, лежащий в верхней полуплоскости, с вырезами в нуле и $-1$. Тогда не придется возиться с квадратом.

[Edmonton]

ex-math в сообщении #935874 писал(а):

Вам надо учесть, что точка $1-i 0$ -- особая, и обойти ее по маленькой полуокружности. Разве Вы не заметили, что не все из использованных Вами интегралов сходятся?

-- 25.11.2014, 11:54 --

Я бы еще посоветовал рассмотреть в качестве области полукруг, лежащий в верхней полуплоскости, с вырезами в нуле и $-1$. Тогда не придется возиться с квадратом.

Правильно ли я понимаю, что Вы рекомендуете рассмотреть область $G(r,R)=C_R(0)\backslash\{\overline{C_r(-1)}\cup \ \overline{C_r(0)} \cup \overline{C_r(1)} \cup [-R;R] \}$, где $C_R (z_0) = \{z: |z-z_0|<R, \operatorname{Im} z \ge 0 \} $? Если я правильно понял, то в этом случае при $f(z) = \frac{h(z)}{z^2-1}$я получаю

$$\int_{\partial G}f(z)dz = \int_{C_R (0)} f(z)dz + \int_{-R}^{-r-1}f(z)dz + \int_{C_r^-(-1)}f(z)dz +\int_{-1+r}^{-r} f(z)dz +\int_{C^-_r(0)} f(z)dz + $$

$$+\int_r^{1-r} f(z)dz+\int_{C^-_r(1)}f(z)dz+\int_{r+1}^R f(z)dz,$$

и всё это по теореме Коши о вычетах равно нулю?

Вроде как большой и маленький интегралы с центром в нуле обнуляются, но как в этом случае быть с маленькими интегралами в центре $\pm 1?$

Да и к тому же разве в этом случае не выйдет, что интеграл с логарифмом при $z<0$ не взаимоуничтожится с интегралом с логарифмом при $z>0?$

[ex-math]

Насчет взаимоуничтожения -- проверьте, это быстро.
В единице у нас устранимая особая точка, а в минус единице -- полюс 1-го порядка. Разложите подынтегральную функцию в ряд Лорана и посмотрите, что останется от интегралов при $r\to+0$.

-- 25.11.2014, 12:51 --

В смысле формально разложите, коэффициенты (кроме вычета) считать не надо.

[Edmonton]

ex-math в сообщении #935888 писал(а):

Насчет взаимоуничтожения -- проверьте, это быстро.
В единице у нас устранимая особая точка, а в минус единице -- полюс 1-го порядка. Разложите подынтегральную функцию в ряд Лорана и посмотрите, что останется от интегралов при $r\to+0$.

1) При $r \to +0,\, R \to +\infty: \;\int_{\partial G} f(z)dz = \int _{-\infty}^0 \frac{\ln (-t)+\pi i}{t^2-1}dt+\int_0^{\infty} \frac{\ln z}{z^2-1}dz; $ делаем замену $z=-t$ в первом интеграле и получаем:

$$\int_{\partial G} f(z)dz = - \int_{+\infty}^0 \frac{\ln z +\pi i}{z^2-1}dz+\int_0^{+\infty} \frac{\ln z}{z^2-1}dz = 2\int_0^{+\infty} \frac{\ln z}{z^2-1}dz + \pi i \int_0^{+\infty} \frac{1}{z^2-1} dz. $$

Выходит, если я тут не ошибся, то они не взаимоуничтожатся, Вы были правы.

2) При $z \to 1:$

$$ \frac{\ln z}{z^2-1} = /* z = 1+t */ = \frac{\ln (t+1)}{t^2 +2\cdot t} = \frac{1}{2t}\frac{\ln (t+1)}{1+\frac{t}{2}}=\frac{1}{2t}(t-\frac{t^2}{2}+\ldots)\cdot (1-\frac{t}{2}+\ldots) $$

При $z \to -1: $

$$\frac{\ln (-z)+\pi i}{z^2-1}= /* z=t-1*/ = \frac{\ln (1-t) +\pi i}{t(t-2)} = \frac{\ln (1-t) +\pi i}{-2t(1-\frac{t}{2})}=\frac{-1}{2t}(\pi i - t - \ldots)(1+\frac{t}{2}+\ldots) $$

Но я пока не понимаю, как из этих данных вытащить значение интегралов по полуокружностям.

[ex-math]

В первом пункте у Вас интегралы (кроме того, который Вы ищете, так как у него особенность в единице устранимая и он сходится в обычном смысле) должны пониматься в смысле главного значения, например

$$ {\mathrm {v.p.}}\int_0^{\infty}\frac{dx}{x^2-1}=\lim_{\varepsilon\to+0}\left(\int_0^{1-\varepsilon}\frac{dx}{x^2-1}+\int_{1+\varepsilon}^{\infty}\frac{dx}{x^2-1}\right). $$

Кстати, этот интеграл табличный и его легко вычислить.

Ряд Лорана в нашем случае состоит из членов вида $c_n(z+1)^n$, где $n=-1,0,\dots$. Проинтегрируйте каждый член по полуокружности с центром в точке $-1$, лежащей в верхней полуплоскости, и посмотрите, что будет, если радиус устремить к нулю. Коэффициенты считать не надо, прямо $c_n(z+1)^n$ и интегрируйте. Аналогично в единице.

-- 25.11.2014, 13:44 --

Пожалуй, проще будет не через ряд Лорана, а чуть по-другому.
В единице у нас устранимая особенность, стало быть, подынтегральная функция ограничена в окрестности единицы. Тут Вы можете тривиально оценить интеграл по полуокружности и увидеть, что он стремится к нулю.
В минус единице, если вычесть главную часть, то будет все то же, что и в единице. Ну а главную часть проинтегрируйте точно.

[Slow]

Так как в $z=-1$ полюс первого порядка можно воспользоваться леммой о полувычете.

[Edmonton]

ex-math в сообщении #935911 писал(а):

В первом пункте у Вас интегралы (кроме того, который Вы ищете, так как у него особенность в единице устранимая и он сходится в обычном смысле) должны пониматься в смысле главного значения, например

$$ {\mathrm {v.p.}}\int_0^{\infty}\frac{dx}{x^2-1}=\lim_{\varepsilon\to+0}\left(\int_0^{1-\varepsilon}\frac{dx}{x^2-1}+\int_{1+\varepsilon}^{\infty}\frac{dx}{x^2-1}\right). $$

Кстати, этот интеграл табличный и его легко вычислить.

Ряд Лорана в нашем случае состоит из членов вида $c_n(z+1)^n$, где $n=-1,0,\dots$. Проинтегрируйте каждый член по полуокружности с центром в точке $-1$, лежащей в верхней полуплоскости, и посмотрите, что будет, если радиус устремить к нулю. Коэффициенты считать не надо, прямо $c_n(z+1)^n$ и интегрируйте. Аналогично в единице.

-- 25.11.2014, 13:44 --

Пожалуй, проще будет не через ряд Лорана, а чуть по-другому.
В единице у нас устранимая особенность, стало быть, подынтегральная функция ограничена в окрестности единицы. Тут Вы можете тривиально оценить интеграл по полуокружности и увидеть, что он стремится к нулю.
В минус единице, если вычесть главную часть, то будет все то же, что и в единице. Ну а главную часть проинтегрируйте точно.

Да, согласен, в смысле главного значения, и в этом смысле он сходится к нулю, но неточность в его задании была вызвана тем, что на ответ в конкретно данной задаче он никакого влияния не оказывает.

Для интегралов у меня следующие рассуждения:
1) $z \to 1,$ тогда $|\int\limits_{C_r^-(1)}f(z)dz \le \int\limits_{C_r(1)}\frac{|\ln (1+r)|}{|(1+r)^2-1|}|dz| \le c_1 \cdot \int_{C_r(1)}\frac{r}{r^2+2r}|dz|\le c_1 \cdot c_2 \frac{1}{2}\int_{C_r(0)} |dz| $ $= \frac{c_1 \cdot c_2 \cdot 2 \pi r}{2} \to 0$ при $r\to +0$

2) При $z \to -1 $ рассматриваем $\int _{C_r^-(-1)} c_{-1}\frac{dz}{1+z}.$ Делаем замену $z=t-1$ и получаем $c_{-1} \int_{C_r^-(0)} \frac{dt}{t}.$ Делаем новую замену $ t=re^{i\varphi}, \,dt = ir\cdot e^{i\varphi} d{\varphi}.$ Получается интеграл $c_{-1}\int^0_{\pi} \frac{i r e^{i\varphi}}{re^{i\varphi}} d \varphi = c_{-1} \cdot i \int^0_{\pi} d\varphi = - c_{-1}\cdot i \cdot \pi.$ Т.к. $c_{-1}=\frac{-\pi i}{2},$ то этот интеграл оказывается равен $\frac{\pi i}{2} \cdot i \cdot \pi = \frac {- \pi^2}{2}$

Таким образом, выходит, что $2I + \frac{- \pi^2}{2} = 0$.

Откуда ответ

$I = \frac{\pi^2}{4}$

И это вроде бы тот самый ответ, который и должен получаться при нормальном решении. Но в таком случае у меня вопрос - если я тут нигде не ошибся, то где была допущена ошибка в первом варианте моего решения, если в точке $1$ интеграл по полуокружности всё равно 0, а побочный интеграл в смысле главного значения сходится к нулю?

[ex-math]

Все верно. В единице достаточно было просто сказать, что раз функция ограничена в окрестности, то интеграл $\leqslant C\cdot\pi r$. Для минус единицы Вы фактически доказали ту самую лемму о полувычете. В будущем, если у Вас полюс первого порядка обходится по дуге окружности, можете в пределе смело писать вычет, умноженный на угловую меру дуги и на $i$, с учетом направления обхода.

Ваша ошибка была в том, что Ваш контур проходил через особую точку $1-i0$ на нижнем берегу разреза. Если обойти ее по малой полуокружности, это даст Вам недостающие $\pi^2/2$.