Подходят линейный функции с рациональными коэффициентами.
Если степень многочлена больше 1 тогда:
1.

, где
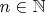
имеет решение при любом

. Тогда все коэффициенты многочлена - рациональные числа.
2.Знаменатели рациональных решений ограниченны, так как они делители произведения первого коэффициента многочлена умноженного на НОК знаменателей всех коэффициентов.
3. При больших

действительных будет 1 действительное решение.(многочлен обязан быть нечетной степени) Если

,

, то разность между

и

стремится к 0(здесь используется то что степень многочлена больше 1), но это не возможно в силу пункта 2.



